题目内容
12.已知$\overrightarrow{AB}$,$\overrightarrow{AC}$均为非零向量,$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=2,点M是线段BC(含两端点)上的一点,且$\overrightarrow{AM}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=1,则|$\overrightarrow{AM}$|的取值范围是A={x|$\frac{1}{8}$≤x≤1}的充分不必要条件(填“充分不必要”,“必要不充分”,“充分必要”,“既不充分也不必要”四者之一).分析 解如图所示,由$\overrightarrow{AB}$,$\overrightarrow{AC}$均为非零向量,$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=2,可得AB⊥AC,BC=2.设P是BC的中点,则$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AP}$.AP=$\frac{1}{2}BC$=1.设$<\overrightarrow{AM},\overrightarrow{AP}>$=θ.由于$\overrightarrow{AM}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=1,可得$|\overrightarrow{AM}|cosθ$=$\frac{1}{2}$,即可得出.
解答 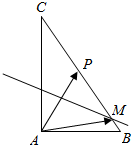 解:如图所示,
解:如图所示,
∵$\overrightarrow{AB}$,$\overrightarrow{AC}$均为非零向量,$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=2,
∴AB⊥AC,BC=2.
设P是BC的中点,则$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AP}$.
AP=$\frac{1}{2}BC$=1.
$<\overrightarrow{AM},\overrightarrow{AP}>$=θ.
∵$\overrightarrow{AM}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=1,
∴$|\overrightarrow{AM}|cosθ$=$\frac{1}{2}$,
∴点M在AP的中垂线上运动,又M点在BC上,
∴1≥$|\overrightarrow{AM}|$$>\frac{1}{2}$.
∴|$\overrightarrow{AM}$|的取值范围是A={x|$\frac{1}{8}$≤x≤1}的“充分不必要”.
故答案为:充分不必要.
点评 本题考查了向量的数量积运算性质、向量的三角形法则、直角三角形的性质,考查了推理能力与计算能力,属于中档题.

| A. | 1 | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{4}$或1 | D. | -1 |
| A. | f(x)g(x)是偶函数 | B. | |f(x)|g(x) 是奇函数 | C. | |f(x)g(x)|是奇函数 | D. | f(|x|)是偶函数 |
| A. | 5 | B. | 7 | C. | 2$\sqrt{2}$ | D. | 9 |
| A. | (3,-2) | B. | (3,2) | C. | (-3,-2) | D. | (2,-3) |
| A. | ±3 | B. | 3 | C. | ±6 | D. | 6 |
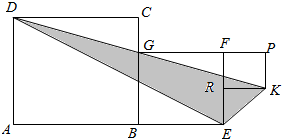 正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )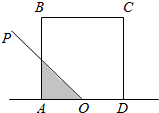 如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论:
如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论: