题目内容
在三棱锥P-ABC中,给出下列四个命题:①如果PA⊥BC,PB⊥AC,那么点P在平面ABC内的射影是△ABC的垂心;
②如果点P到△ABC的三边所在直线的距离都相等,那么点P在平面ABC内的射影是△ABC的内心;
③如果棱PA和BC所成的角为60°,PA=BC=2,E、F分别是棱PB、AC的中点,那么EF=1;
④如果三棱锥P-ABC的各条棱长均为1,则该三棱锥在任意一个平面内的射影的面积都不大于
 .
.其中正确命题的序号是 .
【答案】分析:根据题意画出图形,然后对应选项一一判定即可①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,②若PA=PB=PC,易得AH=BH=CH,则H是△ABC的外心,③如果棱PA和BC所成的角为60°,PA=BC=2,E、F分别是棱PB、AC的中点,那么EF=1或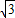 ;不正确.④如果三棱锥P-ABC的各条棱长均为1,则该三棱锥在任意一个平面内的射影的面积的最大值为
;不正确.④如果三棱锥P-ABC的各条棱长均为1,则该三棱锥在任意一个平面内的射影的面积的最大值为 .
.
解答: 解:①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
解:①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
②若PA=PB=PC,易得AH=BH=CH,则H是△ABC的外心,正确.
③如果棱PA和BC所成的角为60°,PA=BC=2,E、F分别是棱PB、AC的中点,那么EF=1或 ;不正确.
;不正确.
④如果三棱锥P-ABC的各条棱长均为1,则该三棱锥在任意一个平面内的射影的面积都不大于 ,正确.
,正确.
故答案为:①②④.
点评:本题考查棱锥的结构特征,考查学生发现问题解决问题的能力,射影定理的应用等,是中档题.
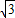 ;不正确.④如果三棱锥P-ABC的各条棱长均为1,则该三棱锥在任意一个平面内的射影的面积的最大值为
;不正确.④如果三棱锥P-ABC的各条棱长均为1,则该三棱锥在任意一个平面内的射影的面积的最大值为 .
.解答:
 解:①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
解:①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.②若PA=PB=PC,易得AH=BH=CH,则H是△ABC的外心,正确.
③如果棱PA和BC所成的角为60°,PA=BC=2,E、F分别是棱PB、AC的中点,那么EF=1或
 ;不正确.
;不正确.④如果三棱锥P-ABC的各条棱长均为1,则该三棱锥在任意一个平面内的射影的面积都不大于
 ,正确.
,正确.故答案为:①②④.
点评:本题考查棱锥的结构特征,考查学生发现问题解决问题的能力,射影定理的应用等,是中档题.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中, 在三棱锥P-ABC中,AB=3,BC=4,AC=5,PA=1 面PAB⊥面CAB,面PAC⊥面CAB,则三棱锥P-ABC的体积是( )
在三棱锥P-ABC中,AB=3,BC=4,AC=5,PA=1 面PAB⊥面CAB,面PAC⊥面CAB,则三棱锥P-ABC的体积是( ) 在三棱锥P-ABC中,PA⊥平面ABC.
在三棱锥P-ABC中,PA⊥平面ABC. (2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
(2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.