题目内容
设函数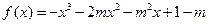 (其中
(其中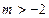 )的图象在
)的图象在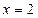 处的切线与直线
处的切线与直线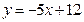 平行.
平行.
(1)求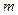 的值;
的值;
(2)求函数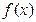 在区间[0,1]的最小值;
在区间[0,1]的最小值;
(3)若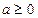 ,
, ,
,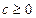 ,且
,且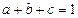 ,试根据上述(1)、(2)的结论证明:
,试根据上述(1)、(2)的结论证明: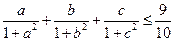 .
.
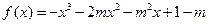 (其中
(其中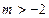 )的图象在
)的图象在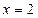 处的切线与直线
处的切线与直线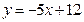 平行.
平行.(1)求
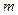 的值;
的值;(2)求函数
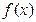 在区间[0,1]的最小值;
在区间[0,1]的最小值;(3)若
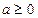 ,
, ,
,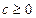 ,且
,且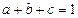 ,试根据上述(1)、(2)的结论证明:
,试根据上述(1)、(2)的结论证明: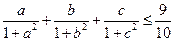 .
. (1)m=-1 (2)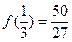 (3)略
(3)略
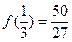 (3)略
(3)略(1)因为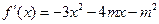 , 所以
, 所以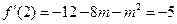 …2分
…2分
解得m=-1或m=-7(舍),即m=-1 …3分
(2)由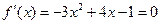 ,解得
,解得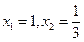 ……………4分
……………4分
列表如下:
所以函数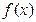 在区间[0,1]的最小值为
在区间[0,1]的最小值为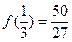 …7分
…7分
(3)因为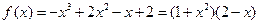
由(2)知,当x∈[0,1]时,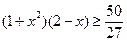 ,所以
,所以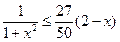 ,
,
所以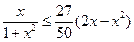 …9分
…9分
当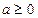 ,
, ,
,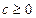 ,且
,且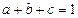 时,
时, 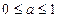 ,
,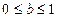 ,
,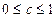 ,
,
所以
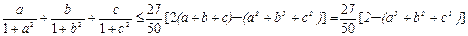 …10分
…10分
又因为
 ,
,
所以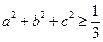 …11分
…11分
故 (当且仅当
(当且仅当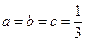 时取等号) …12分
时取等号) …12分
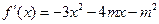 , 所以
, 所以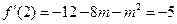 …2分
…2分解得m=-1或m=-7(舍),即m=-1 …3分
(2)由
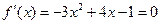 ,解得
,解得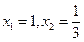 ……………4分
……………4分列表如下:
| x | 0 | (0,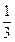 ) ) | 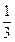 | (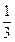 ,1) ,1) | 1 |
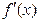 | | - | | + | |
| f(x) | 2 | ↘ |  | ↗ | 2 |
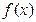 在区间[0,1]的最小值为
在区间[0,1]的最小值为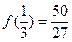 …7分
…7分 (3)因为
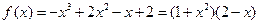
由(2)知,当x∈[0,1]时,
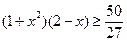 ,所以
,所以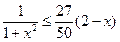 ,
,所以
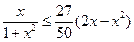 …9分
…9分当
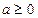 ,
, ,
,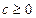 ,且
,且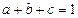 时,
时, 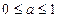 ,
,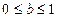 ,
,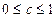 ,
,所以
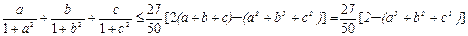 …10分
…10分又因为
 ,
,所以
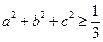 …11分
…11分故
 (当且仅当
(当且仅当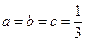 时取等号) …12分
时取等号) …12分
练习册系列答案
相关题目
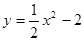 在点
在点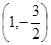 处的切线的倾斜角为
处的切线的倾斜角为



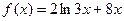 ,则
,则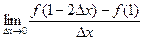 的值为 。
的值为 。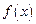 在
在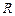 上满足
上满足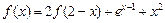 ,则曲线
,则曲线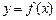 在点
在点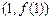 处的切线方程是
处的切线方程是 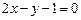
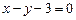
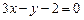
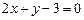
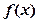 的导函数为
的导函数为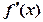 ,且满足
,且满足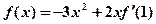 ,则
,则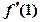 =( )
=( )
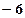
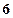
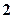
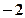
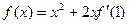 ,则
,则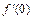 等于( )
等于( )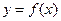 的图象在点
的图象在点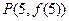 处的切线方程是
处的切线方程是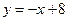 ,则
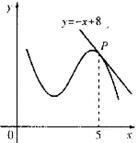
,则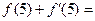 ( )
( )
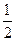

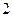
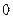
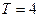 为周期的函数
为周期的函数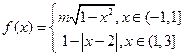 ,其中
,其中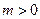 。若方程
。若方程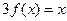 恰有5个实数解,则
恰有5个实数解,则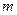 的取值范围为
的取值范围为 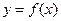 为
为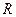 上的连续可导的函数,当
上的连续可导的函数,当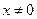 时,
时,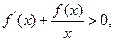 则关于
则关于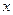 的方程
的方程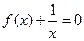 的根的个数为( )
的根的个数为( )