题目内容
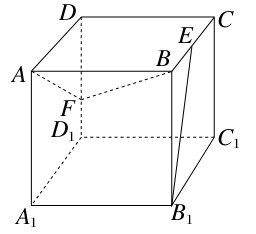
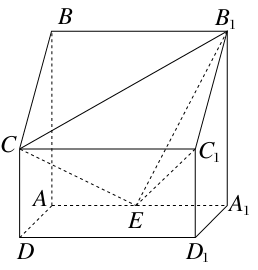
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是棱BC、DD1上的点,如果B1E⊥平面ABF,则CE与DF的和的值为________.

1
以D1A1、D1C1、D1D分别为x,y,z轴建立空间直角坐标系,设CE=x,DF=y,则易知E(x,1,1),B1(1,1,0),∴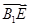 =(x-1,0,1),又F(0,0,1-y),B(1,1,1),∴
=(x-1,0,1),又F(0,0,1-y),B(1,1,1),∴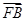 =(1,1,y),由于AB⊥B1E,故若B1E⊥平面ABF,只需
=(1,1,y),由于AB⊥B1E,故若B1E⊥平面ABF,只需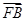 ·
·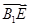 =(1,1,y)·(x-1,0,1)=0⇒x+y=1.
=(1,1,y)·(x-1,0,1)=0⇒x+y=1.
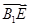 =(x-1,0,1),又F(0,0,1-y),B(1,1,1),∴
=(x-1,0,1),又F(0,0,1-y),B(1,1,1),∴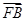 =(1,1,y),由于AB⊥B1E,故若B1E⊥平面ABF,只需
=(1,1,y),由于AB⊥B1E,故若B1E⊥平面ABF,只需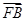 ·
· =(1,1,y)·(x-1,0,1)=0⇒x+y=1.
=(1,1,y)·(x-1,0,1)=0⇒x+y=1.
练习册系列答案
相关题目
 ,求线段AM的长.
,求线段AM的长.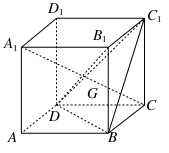
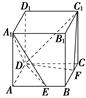
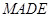 的边长为2,
的边长为2,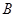 ,
,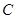 分别为
分别为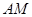 ,
,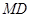 的中点,在五棱锥
的中点,在五棱锥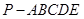 中,
中,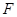 为棱
为棱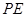 的中点,平面
的中点,平面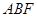 与棱
与棱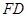 ,
,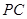 分别交于
分别交于 ,
,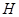 .
.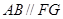 ;
;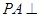 底面
底面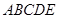 ,且
,且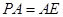 ,求直线
,求直线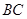 与平面
与平面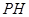 的长.
的长.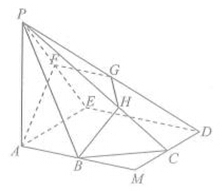
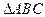
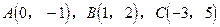
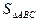 。
。

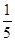

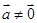 ,
,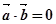 ,则
,则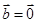 ; ②若
; ②若 ,则
,则 ;
;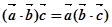 ; ④
; ④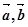 为非零不共线,若
为非零不共线,若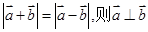 ;
;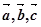 非零不共线,则
非零不共线,则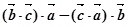 与
与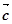 垂直
垂直