题目内容
如图,正方体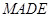 的边长为2,
的边长为2,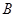 ,
,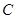 分别为
分别为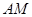 ,
,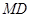 的中点,在五棱锥
的中点,在五棱锥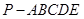 中,
中,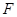 为棱
为棱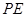 的中点,平面
的中点,平面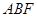 与棱
与棱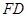 ,
,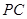 分别交于
分别交于 ,
,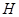 .
.
(1)求证: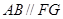 ;
;
(2)若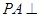 底面
底面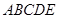 ,且
,且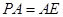 ,求直线
,求直线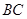 与平面
与平面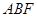 所成角的大小,并求线段
所成角的大小,并求线段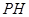 的长.
的长.
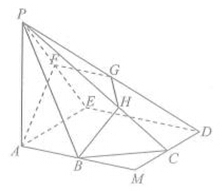
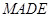 的边长为2,
的边长为2,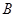 ,
,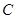 分别为
分别为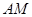 ,
,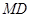 的中点,在五棱锥
的中点,在五棱锥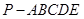 中,
中,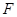 为棱
为棱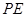 的中点,平面
的中点,平面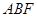 与棱
与棱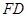 ,
,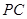 分别交于
分别交于 ,
,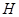 .
.(1)求证:
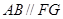 ;
;(2)若
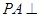 底面
底面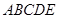 ,且
,且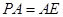 ,求直线
,求直线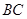 与平面
与平面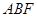 所成角的大小,并求线段
所成角的大小,并求线段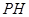 的长.
的长.
(1)详见解析;(2)2.
试题分析:(1)利用正方形的性质,证明
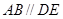 ,利用线面平行的判定定理证明
,利用线面平行的判定定理证明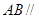 平面
平面 ,再用线面平行的性质定理证明
,再用线面平行的性质定理证明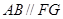 ;(2)由条件
;(2)由条件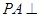 底面
底面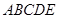 ,证明
,证明 ,
,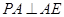 ,
,建立空间直角坐标系
 ,利用向量法求解,先求平面
,利用向量法求解,先求平面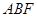 的法向量,利用公式
的法向量,利用公式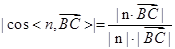 ,求直线
,求直线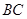 与平面
与平面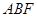 所成的角,再设点
所成的角,再设点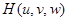 ,因为点
,因为点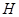 在棱
在棱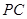 上,所以可设
上,所以可设 ,利用向量的坐标运算,求
,利用向量的坐标运算,求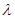 的值,最后用空间中两点间的距离公式求
的值,最后用空间中两点间的距离公式求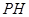 .
.(1)在正方形
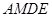 中,因为
中,因为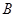 是
是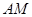 的中点,所以
的中点,所以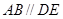 ,
,因为
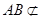 平面
平面 ,所以
,所以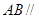 平面
平面 ,
,因为
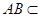 平面
平面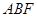 ,且平面
,且平面 平面
平面
 ,
,所以
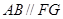 .
.(2)因为
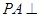 底面
底面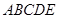 ,所以
,所以 ,
,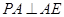 ,
,如图建立空间直角坐标系
 ,则
,则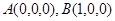 ,
,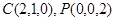 ,
,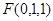 ,
,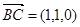 ,设平面
,设平面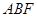 的法向量为
的法向量为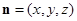 ,
,则
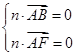 ,即
,即 ,令
,令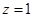 ,则
,则 ,所以
,所以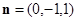 ,
,设直线
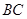 与平面
与平面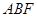 所成的角为
所成的角为 ,则
,则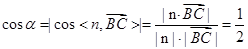 ,
,因此直线
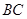 与平面
与平面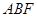 所成的角为
所成的角为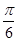 ,
,设点
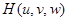 ,因为点
,因为点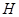 在棱
在棱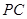 上,所以可设
上,所以可设 ,
,即
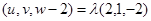 ,所以
,所以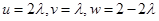 ,
,因为向量
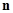 是平面
是平面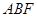 的法向量,所以
的法向量,所以 ,
,即
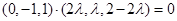 ,解得
,解得 ,所以点
,所以点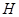 的坐标为
的坐标为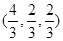 ,
,所以
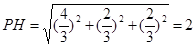 .
.
练习册系列答案
相关题目
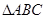 和
和 所在平面互相垂直,且
所在平面互相垂直,且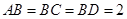 ,
,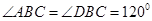 ,E、F分别为AC、DC的中点.
,E、F分别为AC、DC的中点.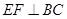 ;
;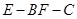 的正弦值.
的正弦值.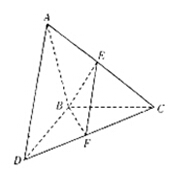
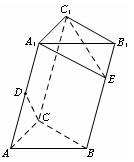
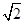 a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.
a,A1C=CA=AB=a,AB⊥AC,D为AA1中点. .
.
 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.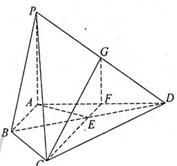
 AB.Q是PC上的一点,且PA∥平面QBD.
AB.Q是PC上的一点,且PA∥平面QBD.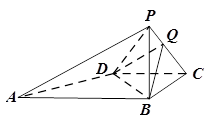
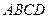 是同一球面上的四点,且每两点间距离相等,都等于2,则球心到平面
是同一球面上的四点,且每两点间距离相等,都等于2,则球心到平面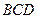 的距离是( )
的距离是( )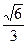
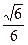

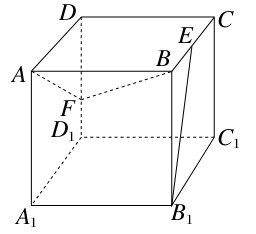
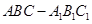 的底面
的底面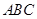 是等腰直角三角形,
是等腰直角三角形,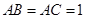 ,侧棱
,侧棱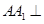 底面
底面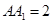 ,
,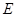 是
是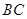 的中点,
的中点,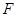 是
是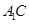 上的点.
上的点.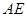 与
与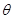 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);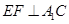 ,求线段
,求线段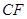 的长.
的长.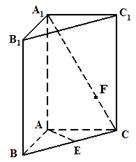
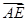 =
=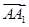 +x
+x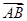 +y
+y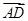 ,则x、y的值分别为( )
,则x、y的值分别为( )