题目内容
(1)(选修4-4坐标系与参数方程)已知曲线C的极坐标方程是ρ=2sinθ,直线l的参数方程是
(t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,则|MN|的最大值为
+1
+1
(2)(选修4-5不等式选讲)设函数f(x)=|x-1|+|x-2|,若不等式|a+b|+|a-b|≥|a|f(x),(a≠0,a,b∈R)恒成立,则实数x的取值范围是
≤x≤
≤x≤
.
|
| 5 |
| 5 |
(2)(选修4-5不等式选讲)设函数f(x)=|x-1|+|x-2|,若不等式|a+b|+|a-b|≥|a|f(x),(a≠0,a,b∈R)恒成立,则实数x的取值范围是
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
分析:(1)首先将曲线C化成普通方程,得出它是以P(0,1)为圆心半径为1的圆,然后将直线L化成普通方程,得出它与x轴的交点M的坐标,最后用两个点之间的距离公式得出PM的距离,从而得出曲C上一动点N到M的最大距离.
(2)先分离出含有a,b的式子,即
(|a+b|+|a-b|)≥f(x)恒成立,问题转化为求左式的最小值即可.
(2)先分离出含有a,b的式子,即
| 1 |
| |a| |
解答:解:(1)∵曲线C的极坐标方程ρ=2sinθ,化成普通方程:
x2+y2-2y=0,即x2+(y-1)2=1
∴曲线C表示以点P(0,1)为圆心,半径为1的圆
∵直L的参数方程是:
∴直L的普通方程是:4x+3y-8=0
∴可得L与x轴的交点M坐标为(2,0)
∴PM=
=
由此可得曲C上一动点N到M的最大距离等于
+1
故答案为:
+1
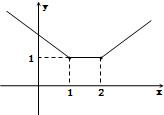 (2)化简得:f(x)=
(2)化简得:f(x)=
,
其图象如图所示,
由|a+b|+|a-b|≥|a|f(x)
得
≥f(x)
又因为
≥
=2
则有2≥f(x)
结合图象解不等式:2≥|x-1|+|x-2|
得
≤x≤
故答案为:
≤x≤
.
x2+y2-2y=0,即x2+(y-1)2=1
∴曲线C表示以点P(0,1)为圆心,半径为1的圆
∵直L的参数方程是:
|
∴直L的普通方程是:4x+3y-8=0
∴可得L与x轴的交点M坐标为(2,0)
∴PM=
| (2-0) 2+(0-1) 2 |
| 5 |
由此可得曲C上一动点N到M的最大距离等于
| 5 |
故答案为:
| 5 |
 (2)化简得:f(x)=
(2)化简得:f(x)=
|
其图象如图所示,
由|a+b|+|a-b|≥|a|f(x)
得
| |a+b|+|a-b| |
| |a| |
又因为
| |a+b|+|a-b| |
| |a| |
| |a+b+a-b| |
| |a| |
则有2≥f(x)
结合图象解不等式:2≥|x-1|+|x-2|
得
| 1 |
| 2 |
| 5 |
| 2 |
故答案为:
| 1 |
| 2 |
| 5 |
| 2 |
点评:(1)本题考查了简单的曲线的极坐标方程和参数方程化为普通方程、以及圆上动点到圆外一个定点的距离最值的知识点.(2)本题主要考查了不等式的恒成立问题,通常采用分离参数的方法解决,属于基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)