题目内容
选修4~4:坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(I)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A,B.若点P的坐标为(1,2),求|PA|+|PB|的最小值.
在直角坐标系xOy中,直线l的参数方程为
|
(I)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A,B.若点P的坐标为(1,2),求|PA|+|PB|的最小值.
分析:(I)利用x=ρcosθ,y=ρsinθ可将圆C极坐标方程化为直角坐标方程;
(II)先根据(I)得出圆C的普通方程,再根据直线与交与交于A,B两点,可以把直线与曲线联立方程,用根与系数关系结合直线参数方程的几何意义,表示出|PA|+|PB|,最后根据三角函数的性质,即可得到求解最小值.
(II)先根据(I)得出圆C的普通方程,再根据直线与交与交于A,B两点,可以把直线与曲线联立方程,用根与系数关系结合直线参数方程的几何意义,表示出|PA|+|PB|,最后根据三角函数的性质,即可得到求解最小值.
解答:解:(Ⅰ)由ρ=6sinθ得ρ2=6ρsinθ,化为直角坐标方程为x2+y2=6y,即x2+(y-3)2=9.
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得t2+2(cosα-sinα)t-7=0.
由△=(2cosα-2sinα)2+4×7>0,故可设t1,t2是上述方程的两根,
所以
又直线l过点(1,2),
故结合t的几何意义得|PA|+|PB|=|t1|+|t2|=|t1-t2|=
=
=
≥
=2
.
所以|PA|+|PB|的最小值为2
.
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得t2+2(cosα-sinα)t-7=0.
由△=(2cosα-2sinα)2+4×7>0,故可设t1,t2是上述方程的两根,
所以
|
故结合t的几何意义得|PA|+|PB|=|t1|+|t2|=|t1-t2|=
| (t1+t2)2-4t1t2 |
| 4(cosα-sinα)2+28 |
| 32-4sin2α |
| 32-4 |
| 7 |
所以|PA|+|PB|的最小值为2
| 7 |
点评:此题主要考查参数方程的优越性,及直线与曲线相交的问题,在此类问题中一般可用联立方程式后用韦达定理求解即可,属于综合性试题有一定的难度.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
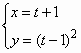 (t为参数);相交于A,B两点,则线段AB的中点的直角坐标为________.
(t为参数);相交于A,B两点,则线段AB的中点的直角坐标为________.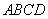 是边长为
是边长为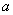 的正方形,以
的正方形,以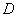 为圆心,
为圆心,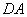 为半径的圆弧与以
为半径的圆弧与以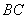 为直径的
为直径的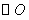 交于点
交于点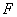 ,延长
,延长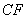 交
交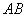 于
于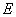 .(1)求证:
.(1)求证: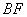 的长.
的长.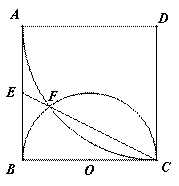
 ,若矩阵
,若矩阵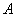 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为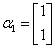 ,属于特征值-1的一个特征向量为
,属于特征值-1的一个特征向量为 ,求矩阵
,求矩阵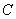 的极坐标方程为
的极坐标方程为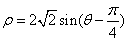 ,以极点为原点,极轴为
,以极点为原点,极轴为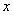 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线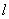 的参数方程为
的参数方程为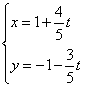 (
(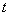 为参数),求直线
为参数),求直线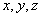 满足
满足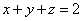 ,求
,求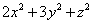 的最小值;
的最小值;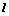 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角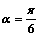 ,
,