题目内容
（2012•葫芦岛模拟）选修4-4：坐标系与参数方程．
在平面直角坐标系中，曲线C1的参数方程为
（a＞b＞0，?为参数），以Ο为极点，x轴的正半轴为极轴建立极坐标系，曲线C2是圆心在极轴上且经过极点的圆，已知曲线C1上的点M（2，
）对应的参数φ=
；θ=
；与曲线C2交于点D（
，
）
（1）求曲线C1，C2的方程；
（2）A（ρ1，θ），Β（ρ2，θ+
）是曲线C1上的两点，求
+
的值．
在平面直角坐标系中，曲线C1的参数方程为
|
| 3 |
| π |
| 3 |
| π |
| 4 |
| 2 |
| π |
| 4 |
（1）求曲线C1，C2的方程；
（2）A（ρ1，θ），Β（ρ2，θ+
| π |
| 2 |
| 1 | ||
|
| 1 | ||
|
分析：（1）将M（2，
）对应的参数φ=
，代入曲线C1的参数方程，求出a、b的值，可得曲线C1的方程．把点D的极坐标化为直角坐标代入圆C2的方程为（x-R）2+y2=R2 ，求得R=1，即可得到曲线C2的方程．
（2）把A、B两点的极坐标化为直角坐标，代入曲线C1的方程可得：
+
=1，
+
=1从而求出
+
的值．
| 3 |
| π |
| 3 |
（2）把A、B两点的极坐标化为直角坐标，代入曲线C1的方程可得：
| ρ12cos2θ |
| 16 |
| ρ12sin2θ |
| 4 |
| ρ22cos2θ |
| 16 |
| ρ22sin2θ |
| 4 |
| 1 | ||
|
| 1 | ||
|
解答：解：（1）将M（2，
）及对应的参数φ=
；θ=
；
代入
得：
得：
∴曲线C1的方程为：
（∅为参数）或
+
=1．
设圆C2的半径R，则圆C2的方程为：ρ=2Rcosθ（或（x-R）2+y2=R2），将点D（
，
）
代入得：
=2R•
∴R=1
∴圆C2的方程为：ρ=2cosθ（或（x-1）2+y2=1）…（5分）
（2）曲线C1的极坐标方程为：
+
=1
将A（ρ?，θ），Β（ρ?，θ+
）代入得：
+
=1，
+
=1
∴
+
=（
+
）+（
+
）=
…（10分）
| 3 |
| π |
| 3 |
| π |
| 4 |
代入
|
|
得：
|
∴曲线C1的方程为：
|
| x2 |
| 16 |
| y2 |
| 4 |
设圆C2的半径R，则圆C2的方程为：ρ=2Rcosθ（或（x-R）2+y2=R2），将点D（
| 2 |
| π |
| 4 |
代入得：
| 2 |
| ||
| 2 |
∴R=1
∴圆C2的方程为：ρ=2cosθ（或（x-1）2+y2=1）…（5分）
（2）曲线C1的极坐标方程为：
| ρ2cos2θ |
| 16 |
| ρ2sin2θ |
| 4 |
将A（ρ?，θ），Β（ρ?，θ+
| π |
| 2 |
| ρ12cos2θ |
| 16 |
| ρ12sin2θ |
| 4 |
| ρ22cos2θ |
| 16 |
| ρ22sin2θ |
| 4 |
∴
| 1 | ||
|
| 1 | ||
|
| cos2θ |
| 16 |
| sin2θ |
| 4 |
| sin2θ |
| 16 |
| cos2θ |
| 4 |
| 5 |
| 16 |
点评：本题主要考查把参数方程化为普通方程的方法，把极坐标方程化为直角坐标方程的方法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
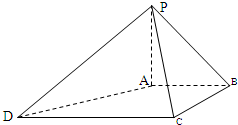（2012•葫芦岛模拟）在四棱锥P-ABCD中，PA⊥底面ABCD，AB∥CD，AB⊥BC，PA=AB=BC=