题目内容
【题目】已知函数![]() ,且
,且![]() .
.
(1)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)因为函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() 恒成立,转化为二次函数
恒成立,转化为二次函数![]() 恒成立问题,得解;(2)令
恒成立问题,得解;(2)令![]() ,
,![]() 恒成立等价于
恒成立等价于![]() 恒成立,利用导数讨论
恒成立,利用导数讨论![]() 的单调性求最值.
的单调性求最值.
试题解析:(1)因为函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() ,
,
即![]() 在
在![]() 上恒成立
上恒成立
当![]() 时,令
时,令![]() 得
得![]() ,
,
①若![]() ,则
,则![]() ,解得
,解得![]() ;②若
;②若![]() ,则
,则![]() ,解得
,解得![]() .
.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)令![]() ,则
,则![]() ,
,
根据题意,当![]() 时,
时,![]() 恒成立.
恒成立.
所以![]() .
.
①当![]() 时,
时,![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符合题意
,所以不符合题意
②当![]() 时,
时,![]() 时,
时,![]() 恒成立.
恒成立.
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符题意.
,所以不符题意.
③当![]() 时,
时,![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是减函数,
上是减函数,
于是“![]() 对任意
对任意![]() 都成立”的充要条件是
都成立”的充要条件是![]() ,
,
即![]() ,解得
,解得![]() ,故
,故![]()
综上,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 |
|
|
|
|
|
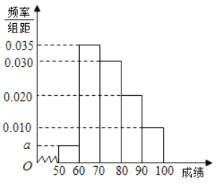
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
【题目】在一次篮球定点投篮训练中,规定每人最多投3次.在![]() 处每投进一球得3分;在
处每投进一球得3分;在![]() 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在![]() 处的投中率
处的投中率![]() ,在
,在![]() 处的投中率为
处的投中率为![]() .该同学选择先在
.该同学选择先在![]() 处投一球,以后都在
处投一球,以后都在![]() 处投,且每次投篮都互不影响.用
处投,且每次投篮都互不影响.用![]() 表示
表示
该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在![]() 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.