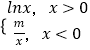题目内容
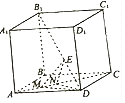
【题目】如图1,在Rt△ABC中,∠C=90°,AC=4,BC=2,D,E分别为边AC,AB的中点,点F,G分别为线段CD,BE的中点.将△ADE沿DE折起到△A1DE的位置,使∠A1DC=60°.点Q为线段A1B上的一点,如图2. 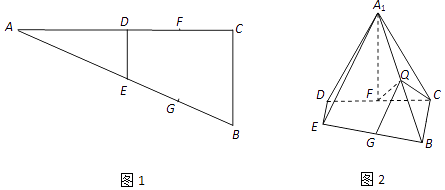
(Ⅰ)求证:A1F⊥BE;
(Ⅱ)线段A1B上是否存在点Q使得FQ∥平面A1DE?若存在,求出A1Q的长,若不存在,请说明理由;
(Ⅲ)当 ![]() 时,求直线GQ与平面A1DE所成角的大小.
时,求直线GQ与平面A1DE所成角的大小.
【答案】解:(Ⅰ)证明:
∵A1D=DC,
∠A1DC=60°,
∴△A1DC为等边三角形,又F为线段CD的中点,
∴A1F⊥DC,
由图1可知ED⊥A1D,ED⊥DC,
∴ED⊥平面A1DC,又A1F平面A1DC,
∴ED⊥A1F,
又ED∩DC=D,DE平面BCDE,CD平面BCDE,
∴A1F⊥平面BCDE,又BE平面BCDE,
所以A1F⊥BE.
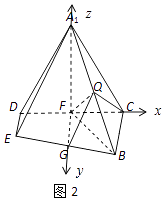
(Ⅱ)取A1B的中点Q,连接FG,FQ,GQ,
∵G,F,Q分别是BE,CD,A1B的中点,
∴FG∥DE,GQ∥A1E,
又FG平面GFQ,GQ平面GFQ,DE平面A1DE,A1E平面A1DE,
∴平面GFQ∥平面A1DE,又FQ平面GFQ,
∴FQ∥平面A1DE.
∴当Q为A1B的中点时,FQ∥平面A1DE.
连接BF,则BF= ![]() =
= ![]() ,
,
由(I)知△A1DC是边长为2的等边三角形,A1F⊥平面BCDE,
∴A1F= ![]() ,A1F⊥BF,
,A1F⊥BF,
∴A1B= ![]() =2
=2 ![]() ,
,
∴A1Q= ![]() =
= ![]() .
.
(Ⅲ)以F为原点,以FC,FG,FA1为坐标轴建立空间直角坐标系,如图所示:
则D(﹣1,0,0),E(﹣1,1,0),A1(0,0, ![]() ),B(1,2,0),G(0,
),B(1,2,0),G(0, ![]() ,0),
,0),
∴ ![]() =(1,2,﹣
=(1,2,﹣ ![]() ),
), ![]() =(0,1,0),
=(0,1,0), ![]() =(1,0,
=(1,0, ![]() ),
), ![]() =(0,﹣
=(0,﹣ ![]() ,
, ![]() ),
),
∴ ![]() =
= ![]() =(
=( ,
![]() ,﹣
,﹣ ![]() ),∴
),∴ ![]() =
= ![]() +
+ ![]() =(
=( ![]() ,0,
,0, ![]() ),
),
设平面A1DE的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 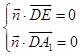 ,
,
∴  ,令z=1得
,令z=1得 ![]() =(﹣
=(﹣ ![]() ,0,1),
,0,1),
∴cos< ![]() >=
>=  =
= 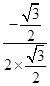 =﹣
=﹣ ![]() ,
,
设直线GQ与平面A1DE所成角为θ,则sinθ=|cos< ![]() >|=
>|= ![]() ,
,
∴直线GQ与平面A1DE所成角为30°.
【解析】(I)由DE⊥平面A1DC得出DE⊥A1F,再证出AF1⊥CD得出A1F⊥平面BCDE,从而得出A1F⊥BE;(II)取A1B的中点Q,连接FG,FQ,GQ,通过中位线证明平面GFQ∥平面A1DE,从而可得FQ∥平面A1DE;(III)以F为原点建立空间坐标系,求出平面A1DE的法向量 ![]() 和
和 ![]() 的坐标,则|cos<
的坐标,则|cos< ![]() >|为所求角的正弦值.
>|为所求角的正弦值.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系和空间角的异面直线所成的角的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则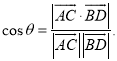 才能正确解答此题.
才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案