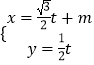题目内容
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1. 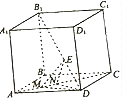
⑴当N为对角线AC的中点且DE= ![]() 时,则三棱锥E﹣DMN的体积是;
时,则三棱锥E﹣DMN的体积是;
⑵当三棱锥E﹣DMN的体积为 ![]() 时,则DE= .
时,则DE= .
【答案】![]() ;
; ![]()
【解析】解:(1)∵底面ABCD是边长为2的正方形,N是AC的中点,
∴AC⊥BD,DN= ![]() ,
,
∵BB1⊥平面ABCD,AC平面ABCD,
∴AC⊥BB1,又BB1∩BD=B,
∴AC⊥平面BB1D,
故当N为AC的中点时,有MN⊥平面DEN,
又DB1=2 ![]() ,BB1=2,∴sin∠BDB1=
,BB1=2,∴sin∠BDB1= ![]() =
= ![]() ,
,
∴VE﹣DMN=VM﹣DEN= ![]() =
= ![]() =
= ![]() .
.
⑵设三棱锥E﹣DMN的高为h,
则VE﹣DMN= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴h= ![]() ,
,
∵ ![]() ,即
,即 ![]() ,∴DE=
,∴DE= ![]() .
.
所以答案是:(1) ![]() ,(2)
,(2) ![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
【题目】(2015·陕西)设某校新、老校区之间开车单程所需时间为T,T只与道路畅通状况有关,对其容量为100的样本进行统计,结果如下:
T(分钟) | 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求T的分布列与数学期望ET;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.