题目内容
16.$\frac{\sqrt{3}tan15°+1}{\sqrt{3}-tan15°}$的值是1.分析 把45°拆成60°-15°,然后利用两角差的正切求得答案.
解答 解:∵tan45°=tan(60°-15°)=$\frac{tan60°-tan15°}{1+tan60°tan15°}=\frac{\sqrt{3}-tan15°}{\sqrt{3}tan15°+1}$.
∴$\frac{\sqrt{3}tan15°+1}{\sqrt{3}-tan15°}$=$\frac{1}{tan45°}=1$.
故答案为:1.
点评 本题考查两角差的正切,考查数学转化思想方法,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.甲、乙两人在一次射击测试中各射靶10次,如图分别是这两人命中环数的直方图,若他们的成绩平均数分别为y1和y2,成绩的标准差分别为s1和s2,则( )
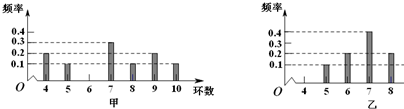

| A. | y1=y2,s1>s2 | B. | y1=y2,s1<s2 | C. | y1>y2,s1=s2 | D. | y1<y2,s1=s2 |
8.若m是2和8的等比中项,则圆锥曲线x2+$\frac{y^2}{m}$=1的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{3}}}{2}$或 $\sqrt{5}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{5}}{2}$ |