题目内容
4.甲、乙两人在一次射击测试中各射靶10次,如图分别是这两人命中环数的直方图,若他们的成绩平均数分别为y1和y2,成绩的标准差分别为s1和s2,则( )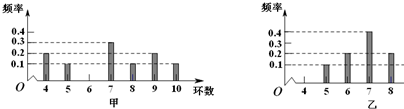
| A. | y1=y2,s1>s2 | B. | y1=y2,s1<s2 | C. | y1>y2,s1=s2 | D. | y1<y2,s1=s2 |
分析 甲乙两位射击运动员在一次射击测试中各射靶10次,根据两人每次射击的环数制成的条形图先分别求出y1,S1和y2,S2,再进行判断.
解答 解:甲乙两位射击运动员在一次射击测试中各射靶10次,
根据两人每次射击的环数制成的条形图知:y1=4×0.2+5×0.1+7×0.3+8×0.1+9×0.2+10×0.1=7,
S1=$\frac{1}{10}$[(7-4)2×2+(7-5)2+(7-7)3×3+(7-8)2+(7-9)2×2+(7-10)2]=4,
y2=5×0.1+6×0.2+7×0.4+8×0.2+9×0.1=7,
s2=$\frac{1}{10}$[(7-5)2+(7-6)2×2+(7-7)2×4+(7-8)2×2+(7-9)2]=1.2,
∴S1>S2,
故选:A.
点评 本题考查频率分布直方图的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
14.给出下边的程序框图,则输出的结果为( )


| A. | $\frac{6}{7}$ | B. | $\frac{5}{6}$ | C. | $\frac{7}{8}$ | D. | $\frac{4}{5}$ |
9.一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有( )颗.


| A. | 3 | B. | 5 | C. | 10 | D. | 27 |
13.凸16边形的对角线条数是( )
| A. | 96 | B. | 104 | C. | 112 | D. | 120 |
14.设全集U=Z,集合M={1,2},P={-2,-1,0,1,2},则P∩CUM=( )
| A. | {0} | B. | {1} | C. | {-1,-2,0} | D. | Φ |