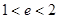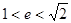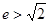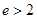题目内容
直线 与圆心为D的圆
与圆心为D的圆 交于A、B两点,则直线AD与BD的倾斜角之和为( )
交于A、B两点,则直线AD与BD的倾斜角之和为( )
A. π π | B. π π | C. π π | D. π π |
C
解析试题分析:根据题目条件画出圆的图象与直线的图象,再利用圆的性质建立两个倾斜角的等量关系,化简整理即可求出
解:直线 的斜率为
的斜率为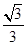 ,所以它的倾斜角为:
,所以它的倾斜角为: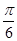 画出直线与圆的图象,
画出直线与圆的图象,
由图象及三角形的外角与不相邻的内角关系,可知:∠1=α-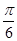 ,∠2=
,∠2=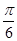 +π-β,由圆的性质可知,直线AD,BD过圆心,三角形ABD是等腰三角形,∴∠1=∠2,∴α-
+π-β,由圆的性质可知,直线AD,BD过圆心,三角形ABD是等腰三角形,∴∠1=∠2,∴α-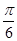 =
=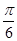 +π-β,故α+β=
+π-β,故α+β= π,故答案为:C
π,故答案为:C
考点:直线与圆相交的性质
点评:本题主要考查了圆的方程与直线方程的位置关系,直线的倾斜角,三角形的角的关系,直线和圆的方程的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
抛物线 的焦点坐标为( ) .
的焦点坐标为( ) .
A. | B. | C. | D. |
若双曲线 与直线
与直线 无交点,则离心率
无交点,则离心率 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
已知椭圆 上的一点
上的一点 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则 到另一焦点距离为
到另一焦点距离为
A. | B. | C. | D. |
 中
中 ,点
,点 的斜坐标定义为:“若
的斜坐标定义为:“若 (其中
(其中 分别为与斜坐标系的
分别为与斜坐标系的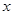 轴,
轴, 轴同方向的单位向量),则点
轴同方向的单位向量),则点 ”.若
”.若 且动点
且动点 满足
满足 ,则点
,则点 在斜坐标系中的轨迹方程为
在斜坐标系中的轨迹方程为



 同一条渐近线上的两个不同的点,已知向量
同一条渐近线上的两个不同的点,已知向量 =(1,0),
=(1,0), ,则双曲线的离心率e等于
,则双曲线的离心率e等于 C.2或
C.2或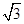 D. 2或
D. 2或 是双曲线
是双曲线 的左焦点,点
的左焦点,点 是该双曲线的右顶点,过
是该双曲线的右顶点,过 轴的直线与双曲线交于
轴的直线与双曲线交于 、
、 两点,若
两点,若 是锐角三角形,则该双曲线的离心率
是锐角三角形,则该双曲线的离心率 的取值范围是( ).
的取值范围是( ).

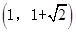

 的离心率为
的离心率为 .双曲线
.双曲线 的渐近线与椭圆
的渐近线与椭圆 有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
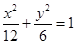


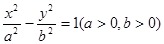 的右焦点F,作渐近线
的右焦点F,作渐近线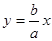 的垂线与双曲线左右两支都相交,则双曲线的离心率
的垂线与双曲线左右两支都相交,则双曲线的离心率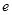 的取值范围为 ( )
的取值范围为 ( )