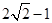题目内容
设A、B为双曲线
同一条渐近线上的两个不同的点，已知向量
=（1，0），
，则双曲线的离心率e等于
A．2 B．
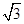C．2或
D． 2或
D
解析试题分析：由已知向量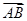
在x轴上的影射长为3。
而|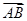|=6，因此A、B点所在的渐进线与x轴的夹角为60°，
有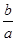
=tan60°或
= tan60°， e=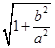
=2或，故选D．
考点：本题主要考查平面向量的数量积，平面向量的投影，双曲线的几何性质。
点评：易错题，本题易忽视双曲线的焦点在不同坐标轴的情况而误选A。a,b,c,e的关系要熟悉，本解法通过e=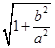计算，免除了解方程组之困。
练习册系列答案
相关题目
已知实数
,
,
构成一个等比数列,则圆锥曲线
的离心率为( )
A． | B． | C． | D． |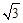
椭圆
的左焦点为F，右顶点为A，以FA为直径的圆经过椭圆的上顶点，则椭圆的离心率为（ ）
A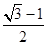． | B． | C． | D． |
以
为中心，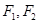
为两个焦点的椭圆上存在一点
，满足
,则该椭圆的离心率为
A． | B． | C． | D． |
已知抛物线
，的焦点为F，直线
与抛物线C交于A、B两点，则
( )
A． | B． | C． | D． |
过抛物线
的焦点F,且和
轴交于点A,若△OAF(O为坐标原点)的面积为4, 则抛物线方程为
直线
与圆心为D的圆
交于A、B两点，则直线AD与BD的倾斜角之和为（ ）
A． π | B． π | C． π | D． π |
和－1，则点C所对应的实数是
已知正三角形AOB的顶点A,B在抛物线
上，O为坐标原点，则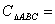
（ ）
A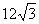． | B． | C． | D． |