题目内容
【题目】
年新型冠状病毒疫情爆发，贵州省教育厅号召全体学生“停课不停学”.自
月
日起，高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果，某中学随机抽取
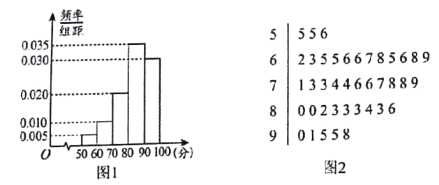
名高三年级学生做“是否准时提交作业”的问卷调查，并组织了一场线上测试，调查发现有
名学生每天准时提交作业，根据他们的线上测试成绩得频率分布直方图(如图
所示)；另外
名学生偶尔没有准时提交作业，根据他们的线上测试成绩得茎叶图(如图所示，单位：分)
（1）成绩不低于
分为
等，低于分为非等.完成以下列联表，并判断是否有
以上的把握认为成绩取得等与每天准时提交作业有关？
准时提交作业与成绩等次列联表 | 单位：人 | ||
A等 | 非A等 | 合计 | |
每天准时提交作业 | |||
偶尔没有准时提交作业 | |||
合计 | |||
（2）成绩低于
分为不合格，从这名学生里成绩不合格的学生中再抽取
人，其中每天准时提交作业的学生人数为
，求的分布列与数学期望.
附：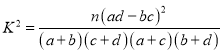
|
|
|
|
|
|
|
|
|
|
【答案】（1）列联表见解析，有
以上的把握认为成绩取得
等与每天准时提交作业有关.（2）分布列见解析，
.
【解析】
（1）根据频率分布直方图计算出每天准时提交作业的等学生人数，再结合茎叶图中的数据可得出
列联表，可计算出
的观测值，利用临界值表可得出结论；
（2）由频率分布直方图和茎叶图可知成绩低于
分的学生共
人，其中每天准时提交作业的有
人，偶尔没有准时提交作业的有
人，可知随机变量
的可能取值有
、
、、
，计算出随机变量在不同取值下的概率，可得出随机变量的分布列，利用期望公式可计算出随机变量的数学期望值.
（1）每天准时提交作业的等学生人数为
，
根据题意得到列联表
A等 | 非A等 | 合计 | |
每天准时提交作业 |
|
|
|
偶尔没有准时提交作业 |
|
|
|
合计 |
|
|
|
，
所以有以上的把握认为成绩取得等与每天准时提交作业有关；
（2）成绩低于分的学生共人，其中每天准时提交作业的有人，偶尔没有准时提交作业的有人，所以随机变量的可能取值有、、、.
，
，
，
.
随机变量的分布列为：
|
|
|
|
|
|
|
|
|
|
随机变量的数学期望为
.
互动英语系列答案
