题目内容
在平面直角坐标系xoy中,椭圆E: (a>0,b>0)经过点A(
(a>0,b>0)经过点A( ,
, ),且点F(0,-1)为其一个焦点.
),且点F(0,-1)为其一个焦点. (Ⅰ)求椭圆E的方程;
(Ⅱ)设椭圆E与y轴的两个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
【答案】分析:(Ⅰ)根据题意可得 解出即可;
解出即可;
(Ⅱ)不妨设A1(0,2),A2(0,-2)
P(x,4)为直线y=4上一点(x≠0),M(x1,y1),N(x2,y2)
直线PA1方程为 ,直线PA2方程为
,直线PA2方程为 ,分别与椭圆联立即可得到点M,N的坐标.
,分别与椭圆联立即可得到点M,N的坐标.
由于椭圆关于y轴对称,当动点P在直线y=4上运动时,直线MN通过的定点必在y轴上,
当x=1时,直线MN的方程为 ,令x=0,得y=1可猜测定点的坐标为(0,1),并记这个定点为B
,令x=0,得y=1可猜测定点的坐标为(0,1),并记这个定点为B
再证明kBM=kBN,即M,B,N三点共线即可.
又F(0,-1),B(0,1)是椭圆E的焦点,利用椭圆的定义即可得出△FMN的周长.
解答: 解:(Ⅰ)根据题意可得
解:(Ⅰ)根据题意可得
可解得
∴椭圆E的方程为 …(4分)
…(4分)
(Ⅱ)不妨设A1(0,2),A2(0,-2)
P(x,4)为直线y=4上一点(x≠0),M(x1,y1),N(x2,y2)
直线PA1方程为 ,直线PA2方程为
,直线PA2方程为
点M(x1,y1),A1(0,2)的坐标满足方程组 可得
可得
点N(x2,y2),A2(0,-2)的坐标满足方程组 可得
可得
由于椭圆关于y轴对称,当动点P在直线y=4上运动时,直线MN通过的定点必在y轴上,
当x=1时,直线MN的方程为 ,令x=0,得y=1可猜测定点的坐标为(0,1),并记这个定点为B
,令x=0,得y=1可猜测定点的坐标为(0,1),并记这个定点为B
则直线BM的斜率kBM= =
= =
=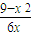
直线BN的斜率kBN= =
= =
=
∴kBM=kBN,即M,B,N三点共线,故直线MN通过一个定点B(0,1),
又∵F(0,-1),B(0,1)是椭圆E的焦点,
∴△FMN周长=|FM|+|MB|+|BN|+|NF|=4b=8.
点评:熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到方程组、三点共线与斜率的关系等是解题的关键.
 解出即可;
解出即可;(Ⅱ)不妨设A1(0,2),A2(0,-2)
P(x,4)为直线y=4上一点(x≠0),M(x1,y1),N(x2,y2)
直线PA1方程为
 ,直线PA2方程为
,直线PA2方程为 ,分别与椭圆联立即可得到点M,N的坐标.
,分别与椭圆联立即可得到点M,N的坐标.由于椭圆关于y轴对称,当动点P在直线y=4上运动时,直线MN通过的定点必在y轴上,
当x=1时,直线MN的方程为
 ,令x=0,得y=1可猜测定点的坐标为(0,1),并记这个定点为B
,令x=0,得y=1可猜测定点的坐标为(0,1),并记这个定点为B再证明kBM=kBN,即M,B,N三点共线即可.
又F(0,-1),B(0,1)是椭圆E的焦点,利用椭圆的定义即可得出△FMN的周长.
解答:
 解:(Ⅰ)根据题意可得
解:(Ⅰ)根据题意可得
可解得

∴椭圆E的方程为
 …(4分)
…(4分)(Ⅱ)不妨设A1(0,2),A2(0,-2)
P(x,4)为直线y=4上一点(x≠0),M(x1,y1),N(x2,y2)
直线PA1方程为
 ,直线PA2方程为
,直线PA2方程为
点M(x1,y1),A1(0,2)的坐标满足方程组
 可得
可得
点N(x2,y2),A2(0,-2)的坐标满足方程组
 可得
可得
由于椭圆关于y轴对称,当动点P在直线y=4上运动时,直线MN通过的定点必在y轴上,
当x=1时,直线MN的方程为
 ,令x=0,得y=1可猜测定点的坐标为(0,1),并记这个定点为B
,令x=0,得y=1可猜测定点的坐标为(0,1),并记这个定点为B则直线BM的斜率kBM=
 =
= =
=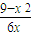
直线BN的斜率kBN=
 =
= =
=
∴kBM=kBN,即M,B,N三点共线,故直线MN通过一个定点B(0,1),
又∵F(0,-1),B(0,1)是椭圆E的焦点,
∴△FMN周长=|FM|+|MB|+|BN|+|NF|=4b=8.
点评:熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到方程组、三点共线与斜率的关系等是解题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是