题目内容
2.已知正四面体的顶点都在表面积为36π的球面上,则此正四面体体积为8$\sqrt{3}$.分析 画出几何图形,求出球的半径,可得正方体的棱长为2$\sqrt{3}$,正方体的体积为24$\sqrt{3}$,即可求得正四面体体积.
解答 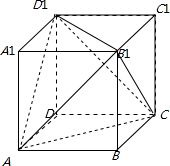 解:正四面体内接于球,则相应的一个正方体内接于球
解:正四面体内接于球,则相应的一个正方体内接于球
设正方体为ABCD-A1B1C1D1,则正四面体为ACB1D1
设球半径为R,则4πR2=36π,∴R=3
∴AC1=6,∴正方体的棱长为2$\sqrt{3}$,正方体的体积为24$\sqrt{3}$,
∴此正四面体体积为24$\sqrt{3}$-4×$\frac{1}{3}$×$\frac{1}{2}$×2$\sqrt{3}$×2$\sqrt{3}$×2$\sqrt{3}$=8$\sqrt{3}$,
故答案为:8$\sqrt{3}$.
点评 本题考查正四面体与正方体的关系,在几何解题中,往往相互联系,本题中采用转化思想,把正四面体的棱长与正方体的棱长,外接球的直径相结合是关键.

练习册系列答案
相关题目
10.函数f(x)=x2-1,则f(1)=( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |