题目内容
13.在△ABC中,角A,B,C所对的边分别为a,b,c,已知$\overrightarrow{m}$=(sinC,sinBcosA),$\overrightarrow{n}$=(b,2c),且$\overrightarrow{m}$•$\overrightarrow{n}$=0(1)求A;
(2)若a=2$\sqrt{3}$,c=2,求△ABC的面积.
分析 (1)根据向量的运算得出bsinC+2csinBcosA=0,利用正弦定理边角转化得出sinBsinC+2sinCsinBcosA=0,约分即可得出cosA=-$\frac{1}{2}$,求解角.
(2)利用余弦定理得出cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=-$\frac{1}{2}$,求解b,利用三角形的面积公式得出即可.
解答 解:(1)∵知$\overrightarrow{m}$=(sinC,sinBcosA),$\overrightarrow{n}$=(b,2c),且$\overrightarrow{m}$•$\overrightarrow{n}$=0
∴bsinC+2csinBcosA=0,①
根据正弦定理得出:b=2RsinB,=2RsinC,代入上式①得出:
sinBsinC+2sinCsinBcosA=0,
1+2cosA=0,
cosA=-$\frac{1}{2}$,
∵0<A<180°
∴A=120°
(2)∵a=2$\sqrt{3}$,c=2,
∴根据余弦定理得出cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=-$\frac{1}{2}$,
即b2+2b-8=0
b=2,b=-4(舍去),
∴S=$\frac{1}{2}$bcsinA=$\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$
点评 本题利用向量考察了三角形的问题,利用正弦定理,余弦定理得出三角形的角,边,考察了学生的运算能力,属于中档题.

练习册系列答案
相关题目
19. 在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )
在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )
 在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )
在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
20.某中学四名高二学生约定“五一”节到本地区三处旅游景点做公益活动,如果每个景点至少一名同学,且甲乙两名同学不在同一景点,则这四名同学的安排情况有( )
| A. | 10种 | B. | 20种 | C. | 30种 | D. | 40种 |
5.按如下程序框图,若输出结果为170,则在判断框内应补充的条件为( )
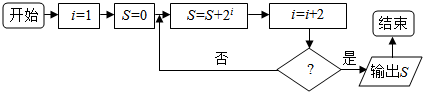

| A. | i≥7 | B. | i>9 | C. | i≥9 | D. | i>10 |
2.计算tan20°+$\frac{2sin40°}{cos20°}$的值为( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
 如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?
如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?