题目内容
如图，在平行四边形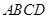
中，边
所在直线的方程为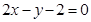
，点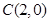
.
（1）求直线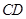
的方程；
（2）求边上的高
所在直线的方程.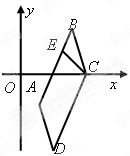
（1）y=2(x-2),即2x-y-4=0（2）x+2y-2=0
解析
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
寒假天地重庆出版社系列答案题目内容
如图，在平行四边形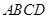中，边所在直线的方程为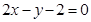，点.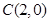
（1）求直线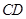的方程；
（2）求边上的高所在直线的方程.
（1）y=2(x-2),即2x-y-4=0（2）x+2y-2=0
解析
寒假天地重庆出版社系列答案
和直线
，求分别满足下列条件的
的值
过点
，并且直线
垂直
轴上的截距为-3
的准线与x轴交于点Q．
与抛物线有公共点，求直线
：
与直线
：
互相平行，经过点
的直线
与
，试求直线
，4）的直线L在两坐标轴上的截距均为正值，当两截距之和最小时，求直线L的方程。
的直线方程；
与
轴的正半轴分别交于
两点，直线
和
分别交于
且平分△
的面积，求
的最小值.