题目内容
设抛物线C：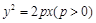
的焦点为F，点M在C上，|MF|＝5，若以MF为直径的圆过点(0, 2)，则C的方程为 ．
或
解析试题分析：依题意可知：
，设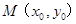
，根据抛物线定义，
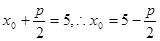因为以
为直径的圆过点
,所以
,
，∴
，∴
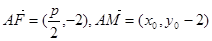又∵点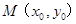在抛物线上，∴
，联立之，可得
，∴
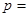2，或8，代入抛物线方程，可得所求抛物线方程为：
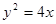或.
考点：1、圆的几何性质；2、抛物线的方程及简单几何性质.
练习册系列答案
相关题目
题目内容
设抛物线C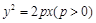：的焦点为F，点M在C上，|MF|＝5，若以MF为直径的圆过点(0, 2)，则C的方程为 ．
或
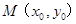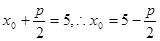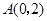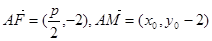解析试题分析：依题意可知：，设，根据抛物线定义，因为以为直径的圆过点,所以,，∴，∴又∵点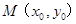在抛物线上，∴，联立之，可得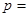，∴2，或8，代入抛物线方程，可得所求抛物线方程为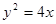：或.
考点：1、圆的几何性质；2、抛物线的方程及简单几何性质.
＋
＝1的左、右焦点，P为椭圆上一点，M是F1P的中点，|OM|＝3，则P点到椭圆左焦点的距离为________．
，若向量
，
，且
，则点
的轨迹C的方程为 
有两个不同的交点，则k的取值范围为 ．
中，椭圆
的中心为原点，焦点
、
在
轴上，离心率为
.过点
交椭圆
、
两点，且
的周长为16，那么椭圆
的渐近线方程是
，那么此双曲线的离心率为 .
与抛物线
的准线相切，则
．
与点
在直线
的两侧，则下列说法：
； 
时，
有最小值，无最大值；
恒成立 
,
, 则
的取值范围为（-