题目内容
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为曲线
的极坐标方程为曲线![]() .
.
(Ⅰ)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求直线![]() 和曲线
和曲线![]() 的两个交点到点
的两个交点到点![]() 的距离的和与积.
的距离的和与积.
【答案】(Ⅰ)![]() 的参数方程为
的参数方程为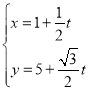 (
(![]() 为参数),
为参数),![]() 的普通方程为
的普通方程为![]() . (Ⅱ)和为
. (Ⅱ)和为![]() ,积为10
,积为10
【解析】
(Ⅰ)利用直线参数方程的标准形式可得直线![]() 的参数方程,利用极坐标方程与普通方程的互化可得曲线
的参数方程,利用极坐标方程与普通方程的互化可得曲线![]() 的普通方程;
的普通方程;
(Ⅱ)将直线参数方程代入圆![]() ,利用韦达定理即可求解.
,利用韦达定理即可求解.
解:(Ⅰ)依题意直线![]() 的参数方程为
的参数方程为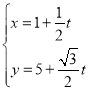 (
(![]() 为参数),
为参数),
曲线![]() 的普通方程为
的普通方程为![]() .
.
(Ⅱ)将直线参数方程代入圆![]() ,
,
化简得出![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 符合为同号且为负值,
符合为同号且为负值,
![]() ,
,
综上所述,直线![]() 和圆
和圆![]() 的两个交点到点
的两个交点到点![]() 的距离的和为
的距离的和为![]() ,积为10.
,积为10.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
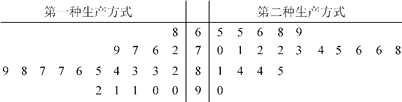
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|