题目内容
已知函数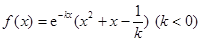 .
.
(Ⅰ)求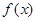 的单调区间;
的单调区间;
(Ⅱ)是否存在实数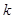 ,使得函数
,使得函数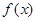 的极大值等于
的极大值等于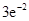 ?若存在,求出
?若存在,求出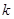 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
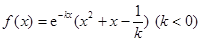 .
.(Ⅰ)求
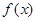 的单调区间;
的单调区间;(Ⅱ)是否存在实数
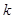 ,使得函数
,使得函数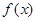 的极大值等于
的极大值等于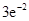 ?若存在,求出
?若存在,求出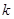 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.解:(Ⅰ)
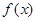 的定义域为
的定义域为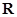 .
.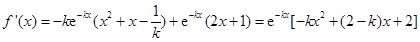 ,
,即
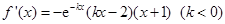 . ………………………………………2分
. ………………………………………2分令
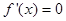 ,解得:
,解得: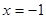 或
或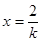 .
. 当
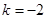 时,
时,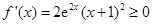 ,故
,故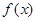 的单调递增区间是
的单调递增区间是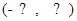 .
.………………………………………3分
当
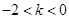 时,
时,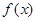 ,
,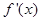 随
随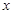 的变化情况如下:
的变化情况如下: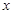 | 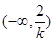 | 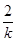 | 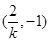 | 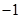 | 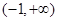 |
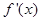 | 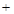 |  | 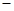 |  | 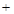 |
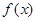 |  | 极大值 |  | 极小值 |  |
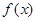 的单调递增区间是
的单调递增区间是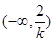 和
和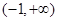 ,单调递减区间是
,单调递减区间是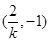 .
.………………………………………5分
当
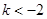 时,
时,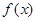 ,
,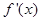 随
随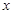 的变化情况如下:
的变化情况如下: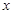 | 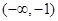 | 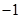 | 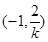 | 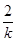 | 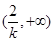 |
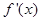 | 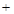 |  | 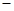 |  | 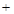 |
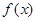 |  | 极大值 |  | 极小值 |  |
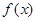 的单调递增区间是
的单调递增区间是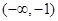 和
和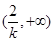 ,单调递减区间是
,单调递减区间是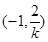 .
.………………………………………7分
(Ⅱ)当
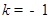 时,
时,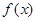 的极大值等于
的极大值等于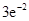 . 理由如下:
. 理由如下:当
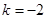 时,
时,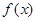 无极大值.
无极大值.当
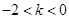 时,
时,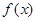 的极大值为
的极大值为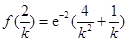 ,
, ………………………………………8分
令
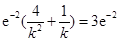 ,即
,即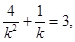 解得
解得 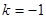 或
或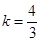 (舍).
(舍).………………………………………9分
当
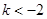 时,
时,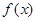 的极大值为
的极大值为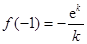 .
. ………………………………………10分
因为
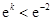 ,
,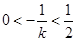 ,
, 所以
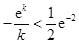 .
.因为
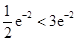 ,
,所以
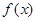 的极大值不可能等于
的极大值不可能等于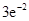 . ………………………………………12分
. ………………………………………12分综上所述,当
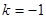 时,
时,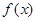 的极大值等于
的极大值等于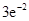 .
.………………………………………13分
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
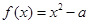 .
.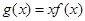 在区间
在区间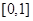 的最小值;
的最小值;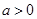 时,记曲线
时,记曲线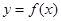 在
在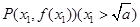 处的切线为
处的切线为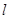 ,
,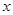 轴交于点
轴交于点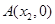 ,求证:
,求证: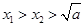 .
.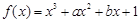 的导函数
的导函数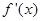 满足
满足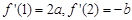 ,其中常数
,其中常数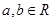 ,则曲线
,则曲线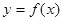 在点
在点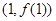 处的切线方程为 。
处的切线方程为 。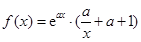 ,其中
,其中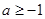 .
.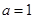 时,求曲线
时,求曲线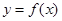 在点
在点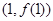 处的切线方程;
处的切线方程;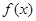 的单调区间.
的单调区间. 在
在 时有极值0,则
时有极值0,则 [o___.
[o___.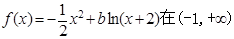 上是减函数,则
上是减函数,则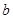 的取值范围是
的取值范围是 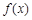 ,若对任意
,若对任意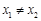 ,都
,都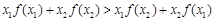 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:①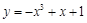 ;②
;② ;③
;③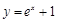 ;④
;④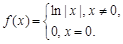 其中是“H函数”的个数为( ).
其中是“H函数”的个数为( ).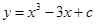 的图像与
的图像与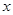 轴恰有两个公共点,则
轴恰有两个公共点,则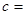 ( )
( )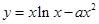 有两个极值点,则实数
有两个极值点,则实数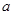 的范围是_____________.
的范围是_____________.