题目内容
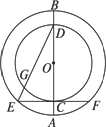
如图,已知两个同心圆O,大圆的直径AB交小圆于C、D两点,大圆的弦EF切小圆于C,ED交小圆于G,若小圆的半径为2,EF=4![]() ,试求EG的长.
,试求EG的长.
答案:
解析:
解析:
|
解:连结GC,则GC⊥ED. 因为EF和小圆切于点C, 所以EF⊥CD,EC= 又CD=4, 所以在Rt△ECD中,有ED= 因为EC2=EG·ED, 所以EG= 分析:由EF和小圆切于点C,易知EF⊥CD.因为CD为小圆的直径,联想“直径所对的圆周角为90°”,考虑连结GC,则GC⊥ED.由已知条件容易求出CD、EC的长.在Rt△ECD中利用勾股定理和射影定理不难求出EG的长. |

练习册系列答案
相关题目
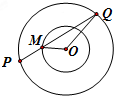 如图,已知两个同心圆的半径分别为1、2,P(x1,y1),Q(x2,y2)是大圆的割线,它与小圆距P最近的公共点是M,则
如图,已知两个同心圆的半径分别为1、2,P(x1,y1),Q(x2,y2)是大圆的割线,它与小圆距P最近的公共点是M,则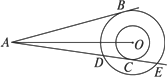

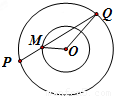 如图,已知两个同心圆的半径分别为1、2,P(x1,y1),Q(x2,y2)是大圆的割线,它与小圆距P最近的公共点是M,则
如图,已知两个同心圆的半径分别为1、2,P(x1,y1),Q(x2,y2)是大圆的割线,它与小圆距P最近的公共点是M,则 的取值范围是 .
的取值范围是 .