题目内容
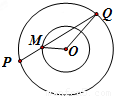 如图,已知两个同心圆的半径分别为1、2,P(x1,y1),Q(x2,y2)是大圆的割线,它与小圆距P最近的公共点是M,则
如图,已知两个同心圆的半径分别为1、2,P(x1,y1),Q(x2,y2)是大圆的割线,它与小圆距P最近的公共点是M,则 的取值范围是 .
的取值范围是 .
【答案】分析:设出M,Q的坐标,求出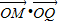 ,结合图象,即可求得取值范围.
,结合图象,即可求得取值范围.
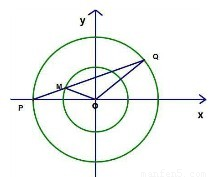
解答:解:设M(cosα,sinα),Q(2cosβ,2sinβ),则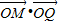 =2cosαcosβ+2sinαsinβ=2cos(α-β)
=2cosαcosβ+2sinαsinβ=2cos(α-β)
如图所示,α-β=∠QOx,则
当PQ与x重合时,(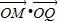 )min=2cosπ=-2;
)min=2cosπ=-2;
当PQ与小圆相切时,(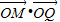 )max=2cos
)max=2cos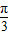 =1,
=1,
∴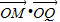 的取值范围是[-2,1]
的取值范围是[-2,1]
故答案为:[-2,1]
点评:本题考查向量的数量积,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.
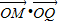 ,结合图象,即可求得取值范围.
,结合图象,即可求得取值范围.解答:解:设M(cosα,sinα),Q(2cosβ,2sinβ),则
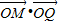 =2cosαcosβ+2sinαsinβ=2cos(α-β)
=2cosαcosβ+2sinαsinβ=2cos(α-β)如图所示,α-β=∠QOx,则

当PQ与x重合时,(
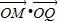 )min=2cosπ=-2;
)min=2cosπ=-2;当PQ与小圆相切时,(
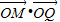 )max=2cos
)max=2cos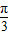 =1,
=1,∴
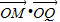 的取值范围是[-2,1]
的取值范围是[-2,1]故答案为:[-2,1]
点评:本题考查向量的数量积,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
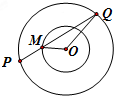 如图,已知两个同心圆的半径分别为1、2,P(x1,y1),Q(x2,y2)是大圆的割线,它与小圆距P最近的公共点是M,则
如图,已知两个同心圆的半径分别为1、2,P(x1,y1),Q(x2,y2)是大圆的割线,它与小圆距P最近的公共点是M,则