题目内容

1．已知（3x-1）7=a7x7+a6x6+…+a1x+a0，则a0+a2+a4+a6=-8128．

分析 通过x=-1与x=1，求出表达式的值，即可求解所求表达式的值．

解答 解：令x=-1，得a0-a1+a2-a3+…+a6-a7=-16384
令x=1，得a0+a1+a2+a3+…+a6+a7=27=128
两式相加：2（a0+a2+a4+a6）=-16256．
a0+a2+a4+a6=-8128
故答案为：-8128．

点评 本题是基础题，考查二项式定理的系数的应用，考查计算能力．

练习册系列答案
相关题目
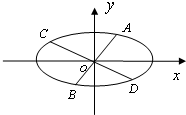17．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的经过中心的弦称为椭圆的一条直径，平行于该直径的所有弦的中点的轨迹为一条直线段，称为该直径的共轭直径．已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1
（Ⅰ）若一条直径的斜率为$\frac{1}{2}$，求该直径的共轭直径所在的直线方程；
（Ⅱ）若椭圆的两条共轭直径为AB和CD，它们的斜率分别为k1、k2，证明：四边形ACBD的面积为定值．
12．若曲线y=x2-aln（x+1）在x=1处取极值，则实数a的值为（　　）
A．1B．2C．3D．4
9．若复数z=$\frac{a+i}{i}$，且z∈R，则实数a=0．
16．函数f（x）=（x-3）ex的单调递增区间是（　　）
A．（2，+∞）B．（0，3）C．（1，4）D．（-∞，2）
6．已知函数f（x）=ax2+bx+1（a，b为实数），设F（x）=$\left\{\begin{array}{l}{f（x），x＞0}\\{-f（x），x＜0}\end{array}\right.$，若f（-1）=0，且对任意实数x均有f（x）≥0成立，求F（x）的表达式．
13．已知$\overrightarrow{a}$=（2，λ），$\overrightarrow{b}$=（sin（2ωx-$\frac{π}{6}$），1），设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（$\frac{1}{2}$，1），若存在x∈（0，$\frac{π}{2}$），使$\overrightarrow{a}$⊥$\overrightarrow{b}$，求λ的取值范围．
10．若正数a，b满足$\frac{1}{a}$+$\frac{1}{b}$=1，则$\frac{1}{a-1}$+$\frac{4}{b-1}$的最小值为（　　）
A．3B．4C．5D．6
11．已知函数f（x）为R上的增函数，函数图象关于点（3，0）对称，若实数x，y满足$f（{x^2}-2\sqrt{3}x+9）+f（{y^2}-2y）≤0$，则$\frac{y}{x}$的取值范围是[0，$\sqrt{3}$]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网