题目内容
下列函数中,是偶函数且在区间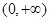 上单调递减的是( ).
上单调递减的是( ).
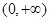 上单调递减的是( ).
上单调递减的是( ).A.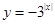 | B.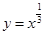 | C.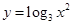 | D.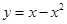 |
A.
由偶函数的定义可知,四个函数中只有
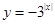 ,
,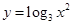 为偶函数。在区间
为偶函数。在区间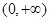 上,
上,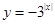 等价于
等价于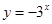 在
在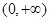 上单调递减,而
上单调递减,而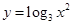 为复合函数,在区间
为复合函数,在区间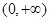 上
上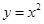 单调递增,值域为
单调递增,值域为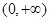 ,而
,而 在区间
在区间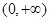 上单调递增,由复合函数单调性“同增异减”可得
上单调递增,由复合函数单调性“同增异减”可得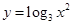 在区间
在区间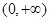 上单调递增。
上单调递增。故选择A

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
题目内容
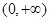 上单调递减的是( ).
上单调递减的是( ).A.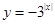 | B.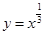 | C.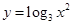 | D.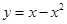 |
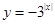 ,
,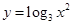 为偶函数。在区间
为偶函数。在区间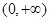 上,
上,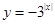 等价于
等价于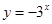 在
在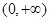 上单调递减,而
上单调递减,而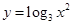 为复合函数,在区间
为复合函数,在区间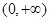 上
上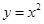 单调递增,值域为
单调递增,值域为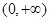 ,而
,而 在区间
在区间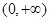 上单调递增,由复合函数单调性“同增异减”可得
上单调递增,由复合函数单调性“同增异减”可得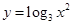 在区间
在区间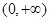 上单调递增。
上单调递增。
 发散思维新课堂系列答案
发散思维新课堂系列答案