题目内容
设定义在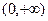 上的函数
上的函数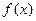 满足下面三个条件:
满足下面三个条件:
①对于任意正实数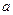 、
、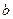 ,都有
,都有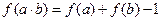 ; ②
; ②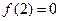 ;
;
③当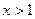 时,总有
时,总有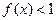 .
.
(1)求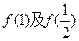 的值;
的值;
(2)求证: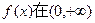 上是减函数.
上是减函数.
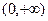 上的函数
上的函数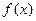 满足下面三个条件:
满足下面三个条件:①对于任意正实数
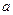 、
、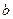 ,都有
,都有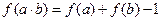 ; ②
; ②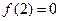 ;
;③当
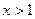 时,总有
时,总有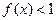 .
.(1)求
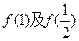 的值;
的值;(2)求证:
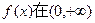 上是减函数.
上是减函数.(1)1;2(2)见解析
(1)取a=b=1,则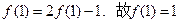
又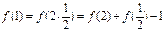 . 且
. 且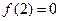 .
.
得: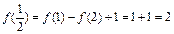
(2)设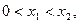 则:
则: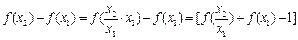
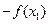
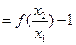 依
依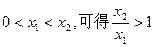
再依据当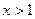 时,总有
时,总有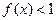 成立,可得
成立,可得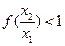
即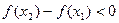 成立,故
成立,故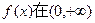 上是减函数。
上是减函数。
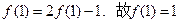
又
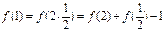 . 且
. 且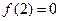 .
.得:
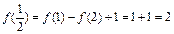
(2)设
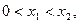 则:
则: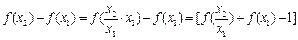
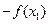
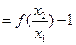 依
依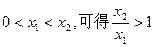
再依据当
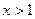 时,总有
时,总有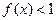 成立,可得
成立,可得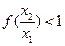
即
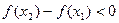 成立,故
成立,故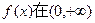 上是减函数。
上是减函数。
练习册系列答案
相关题目
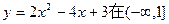 上是单调减函数
上是单调减函数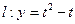 (
(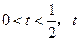 为常数)与函数
为常数)与函数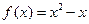 的图象以及y轴所围成的封闭图形的面积为
的图象以及y轴所围成的封闭图形的面积为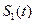 ,若直线l与函数
,若直线l与函数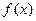 的图象所围成的封闭图形的面积为
的图象所围成的封闭图形的面积为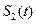 ,已知
,已知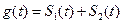 ,当
,当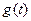 取最小值时,求t的值.
取最小值时,求t的值.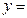
 (
(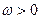 )最小正周期是
)最小正周期是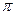 ,求函数
,求函数 的单调递增区间.
的单调递增区间.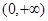 上的增函数的是 ( )
上的增函数的是 ( )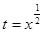
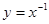
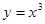
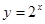
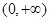 上单调递减的是( ).
上单调递减的是( ).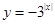
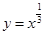
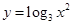
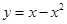
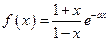 。
。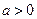 ,讨论
,讨论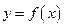 的单调性;
的单调性;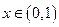 恒有
恒有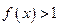 ,求
,求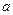 的取值范围。
的取值范围。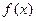 对任意
对任意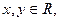 ,都有
,都有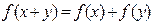 ,
,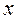 > 0时,
> 0时,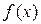 < 0,
< 0,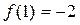 .
. 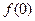 ;
; 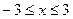 时,
时,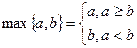 ,设实数
,设实数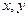 满足约束条件
满足约束条件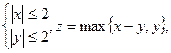 则
则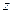 的取值范围是( )。
的取值范围是( )。