题目内容
【题目】椭圆 ![]() 的两顶点为A,B如图,离心率为
的两顶点为A,B如图,离心率为 ![]() ,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.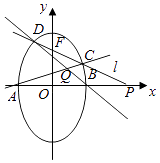
(Ⅰ)当 ![]() 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)当点P异于A,B两点时,求证: ![]() 为定值.
为定值.
【答案】解:(Ⅰ)由题意,设椭圆的标准方程为 ![]() ,
,
由已知得: ![]() ,所以
,所以 ![]() ,椭圆的方程为
,椭圆的方程为 ![]() ,
,
当直线l与x轴垂直时与题意不符,
设直线l的方程为y=kx+1,C1(x1,y1),D(x2,y2),
将直线l的方程代入椭圆的方程化简得(k2+2)x2+2kx﹣1=0,
则 ![]() ,
, ![]() ,∴
,∴ ![]() =
= ![]() ,解得:
,解得: ![]() ,
,
所以直线l的方程为 ![]() ,
,
(Ⅱ)证明:当直线l与x轴垂直时与题意不符,
设直线l的方程为y=kx+1,(k≠0,k≠±1),C(x1,y1),D(x2,y2),∴P点的坐标为 ![]() ,
,
由(Ⅰ)知 ![]() ,
, ![]() ,
,
且直线AC的方程为 ![]() ,且直线BD的方程为
,且直线BD的方程为 ![]() ,
,
将两直线联立,消去y得 ![]() ,
,
∵﹣1<x1,x2<1,∴ ![]() 与
与 ![]() 异号,
异号,
![]() =
= 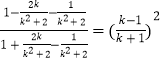 ,
, 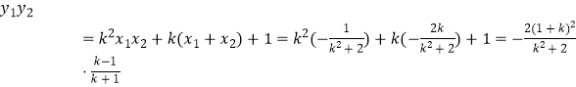 ,
,
∴ ![]() 与y1y2异号,
与y1y2异号, ![]() 与
与 ![]() 同号,
同号,
∴ ![]() ,解得,x=﹣k,
,解得,x=﹣k,
故Q点坐标为(﹣k,y0),
![]() ,
,
故 ![]() 为定值
为定值
【解析】(Ⅰ)根据题意由两点间的距离公式可得,要求出C、D的坐标故可设直线方程与椭圆方程联立用韦达定理即可得到C、D橫坐标之间的关系再代入即可求解直线方程。(Ⅱ)先排除特殊情况再用向量法求解,即设出直线l的方程,联立椭圆方程用韦达定理表示出坐标之间的关系,再代入向量数量积公式即可得证。

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00﹣22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式 | 看电视 | 看书 | 合计 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合计 | 40 | 120 | 160 |
下面临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00﹣22:00时间段的休闲方式与性别有关系”?