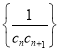题目内容
【题目】(本小题满分10分)
已知如下等式: ![]() ,
, ![]() ,
, ![]() ,
,
当![]() 时,试猜想
时,试猜想![]() 的值,并用数学归纳法给予证明.
的值,并用数学归纳法给予证明.
【答案】解:由已知,猜想![]() ……………………………(2分)
……………………………(2分)
下面用数学归纳法给予证明:
(1)当![]() 时,由已知得原式成立; ………………………………………………(3分)
时,由已知得原式成立; ………………………………………………(3分)
(2)假设当![]() 时,原式成立,即
时,原式成立,即![]() ……(4分)
……(4分)
那么,当![]() 时,
时, ![]()
![]()
![]() =
=![]()
故![]() 时,原式也成立。……………………………………………………(11分)
时,原式也成立。……………………………………………………(11分)
由(1)、(2)知![]() 成立 ……………(12分)
成立 ……………(12分)
【解析】先猜想,然后再用数学归纳法进行证明.
证明时分两个步骤:第一步,先验证是当n=1时,等式是否成立;
第二步,假设n=k时,等式成立;再证明当n=k+1时,等式也成立,再证明时一定要用上归纳假设.否则证明无效


练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.