题目内容
(2013•闸北区二模)和平面解析几何的观点相同,在空间中,空间曲面可以看作是适合某种条件的动点的轨迹.在空间直角坐标系O-xyz中,空间曲面的方程是一个三元方程F(x,y,z)=0.
设F1、F2为空间中的两个定点,|F1F2|=2c>0,我们将曲面Γ定义为满足|PF1|+|PF2|=2a(a>c)的动点P的轨迹.
(1)试建立一个适当的空间直角坐标系O-xyz,求曲面Γ的方程;
(2)指出和证明曲面Γ的对称性,并画出曲面Γ的直观图.
设F1、F2为空间中的两个定点,|F1F2|=2c>0,我们将曲面Γ定义为满足|PF1|+|PF2|=2a(a>c)的动点P的轨迹.
(1)试建立一个适当的空间直角坐标系O-xyz,求曲面Γ的方程;
(2)指出和证明曲面Γ的对称性,并画出曲面Γ的直观图.
分析:(1)以直线F1F2为x轴,线段F1F2的垂直平分线为x轴,以与xoy平面垂直的直线为z轴,建立空间直角坐标系如图.设P的坐标为(x,y,z),根据两点间的距离公式,以a、c为参数建立关于x、y、z的等式,再移项、平方,化简整理得二次方程为
+
+
=1,即为所求曲面Γ的方程;
(2)根据空间关于原点、坐标轴和坐标平面对称的公式,分别对(1)求出的方程加以验证,可得曲面Γ是关于原点对称、关于三条坐标轴对称,也关于三个坐标平面对称的图形.因此不难作出它的直观图,如图所示.
| x2 |
| a2-c2 |
| y2 |
| a2 |
| z2 |
| a2-c2 |
(2)根据空间关于原点、坐标轴和坐标平面对称的公式,分别对(1)求出的方程加以验证,可得曲面Γ是关于原点对称、关于三条坐标轴对称,也关于三个坐标平面对称的图形.因此不难作出它的直观图,如图所示.
解答:解:(1)以两个定点F1,F2的中点为坐标原点O,以F1,F2所在的直线为y轴,以线段F1F2的垂直平分线为x轴,
以与xoy平面垂直的直线为z轴,建立空间直角坐标系O-xyz,如图所示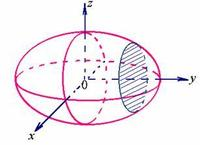
则F1(0,c,0),F2(0,-c,0),设P的坐标为(x,y,z),可得
|F1F2|=2c>0,|
|+|
|=2a(a>c),
∴
+
=2a,
移项得
=2a-
两边平方,得∴a
=a2-cy,
两边平方,整理得
+
+
=1
令
=b,得
+
+
=1.①
因此,可得曲面Γ的方程为
+
+
=1.
(2)对称性:
由于点(x,y,z)关于坐标原点O的对称点(-x,-y,-z)也满足方程①,
说明曲面Γ关于坐标原点O对称;
由于点(x,y,z)关于x轴的对称点(x,-y,-z)也满足方程①,
说明曲面Γ关于x轴对称;同理,曲面Γ关于y轴对称;关于z轴对称.
由于点(x,y,z)关于xOy平面的对称点(x,y,-z)也满足方程①,
说明曲面Γ关于xOy平面对称;同理,曲面Γ关于xOz平面对称;关于yOz平面对称.
由以上的讨论,可得曲面Γ的直观图如右图所示.
以与xoy平面垂直的直线为z轴,建立空间直角坐标系O-xyz,如图所示

则F1(0,c,0),F2(0,-c,0),设P的坐标为(x,y,z),可得
|F1F2|=2c>0,|
| PF1 |
| PF2 |
∴
| x2+(y+c)2+z2 |
| x2+(y-c)2+z2 |
移项得
| x2+(y+c)2+z2 |
| x2+(y-c)2+z2 |
两边平方,得∴a
| x2+(y-c)2+z2 |
两边平方,整理得
| x2 |
| a2-c2 |
| y2 |
| a2 |
| z2 |
| a2-c2 |
令
| a2-c2 |
| x2 |
| b2 |
| y2 |
| a2 |
| z2 |
| b2 |
因此,可得曲面Γ的方程为
| x2 |
| b2 |
| y2 |
| a2 |
| z2 |
| b2 |
(2)对称性:
由于点(x,y,z)关于坐标原点O的对称点(-x,-y,-z)也满足方程①,
说明曲面Γ关于坐标原点O对称;
由于点(x,y,z)关于x轴的对称点(x,-y,-z)也满足方程①,
说明曲面Γ关于x轴对称;同理,曲面Γ关于y轴对称;关于z轴对称.
由于点(x,y,z)关于xOy平面的对称点(x,y,-z)也满足方程①,
说明曲面Γ关于xOy平面对称;同理,曲面Γ关于xOz平面对称;关于yOz平面对称.
由以上的讨论,可得曲面Γ的直观图如右图所示.
点评:本题给出空间满足到两个定点距离之和为定值的点,求该点的轨迹.着重考查了椭圆的定义、轨迹方程求法和曲线与方程的性质等知识,属于中档题.

练习册系列答案
相关题目