题目内容
(2013•闸北区二模)在平面直角坐标系xOy中,以向量
=(a1,a2),
=(b1,b2)为邻边的平行四边形的面积为
| a |
| b |
|a1b2-b1a2|
|a1b2-b1a2|
.分析:设向量
对应
,向量
对应
,由向量模的公式算出|
|和|
|,得到cos∠AOB=
,再由同角三角函数的平方关系算出sin∠AOB的值,最后根据正弦定理的面积公式加以计算,得到平行四边形OACB的面积,即得以向量
、
为邻边的平行四边形的面积值.
| a |
| OA |
| b |
| OB |
| OA |
| OB |
| a1a2+b1b2 | ||||
|
| a |
| b |
解答:解:设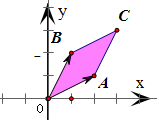 向量
向量
=
=(a1,a2),
=
=(b1,b2)
∴|
|=
,|
|=
可得cos∠AOB=
=
由同角三角函数基本关系,得
sin∠AOB=
=
因此,以
、
为邻边的平行四边形OACB的面积为
S=|
|•|
|sin∠AOB=
•
•
=|a1b2-b1a2|
即以向量
、
为邻边的平行四边形的面积为|a1b2-b1a2|
故答案为:|a1b2-b1a2|
 向量
向量| a |
| OA |
| b |
| OB |
∴|
| OA |
| a12+a22 |
| OB |
| b12+b22 |
可得cos∠AOB=
| ||||
|
|
| a1a2+b1b2 | ||||
|
由同角三角函数基本关系,得
sin∠AOB=
| 1-cos2∠AOB |
| |a1b2-b1a2| | ||||
|
因此,以
| OA |
| OB |
S=|
| OA |
| OB |
| a12+a22 |
| b12+b22 |
| |a1b2-b1a2| | ||||
|
即以向量
| a |
| b |
故答案为:|a1b2-b1a2|
点评:本题给出向量
、
的坐标,求以向量
、
为邻边的平行四边形的面积.着重考查了平面向量数量积计算公式、模的计算公式和平行四边形的面积求法等知识,属于中档题.
| a |
| b |
| a |
| b |

练习册系列答案
相关题目