题目内容
已知函数 .
.
(Ⅰ)解不等式:  ;
;
(Ⅱ)若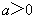 ,求证:
,求证: ≤
≤ .
.
(Ⅰ) (Ⅱ)用绝对值不等式性质证明.
(Ⅱ)用绝对值不等式性质证明.
解析试题分析:(1)由题

 .
.
因此只须解不等式 .
.
当 时,原不式等价于
时,原不式等价于 ,即
,即 .
.
当 时,原不式等价于
时,原不式等价于 ,即
,即 .
.
当 时,原不式等价于
时,原不式等价于 ,即
,即 .
.
综上,原不等式的解集为 .
.
(2)由题
 .
.
当 >0时,
>0时,




考点:绝对值不等式;带绝对值的函数;函数的最值及其几何意义.
点评:本题主要考查绝对值不等式的解法,求函数的最小值的方法,体现了分类讨论与等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度 与时间
与时间 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用. ,求
,求 在
在 处取得极小值.
处取得极小值. 的值;
的值; 在
在 处的切线方程为
处的切线方程为 ,求证:当
,求证:当 时,曲线
时,曲线 不可能在直线
不可能在直线 ,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.  )
) 和
和 的图像如图所示,设两函数的图像交于点
的图像如图所示,设两函数的图像交于点 .
.
 分别对应哪一个函数?
分别对应哪一个函数? ,且
,且 ,指出
,指出 的值,并说明理由;
的值,并说明理由;
 ,及函数
,及函数 。
。 的不等式
的不等式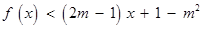 的解集为
的解集为 ,其中
,其中 为正常数。
为正常数。 的值;
的值; R
R 如何取值时,函数
如何取值时,函数

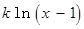 存在极值点,并求出极值点;
存在极值点,并求出极值点; ,且
,且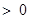 ,求证:
,求证:
 。
。
 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;