题目内容
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为多少时,盒子容积最大,并求出此最大值?
小正方形边长为1时,盒子体积最大为18。
解析试题分析:设小正方形的边长为 厘米,则盒子底面长为
厘米,则盒子底面长为 ,宽为
,宽为
 (
( ) . 6分
) . 6分 ,
, (舍去)
(舍去) ,在定义域内仅有一个极大值,
,在定义域内仅有一个极大值, 
故,小正方形边长为1时,盒子体积最大为18 . 12分
考点:本题主要考查长方体体积公式,函数模型,应用导数研究函数的最值。
点评:中档题,利用长方体体积公式,构建函数模型,再利用导数研究函数的最值,从而解决实际问题。属于常见题目。当函数的驻点只有一个是,这既是极值点,也是最值点。

练习册系列答案
相关题目
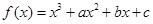 ,曲线
,曲线 在点
在点 处的切线为
处的切线为 ,若
,若 时,
时, 的值;
的值; 上的最大值和最小值.
上的最大值和最小值.
 ;
; 的解集为空集,求
的解集为空集,求 的取值范围.
的取值范围. .
.  ;
; 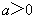 ,求证:
,求证: ≤
≤ .
. 的有铝合金盖的圆柱形铁桶,已知单位面积铝合金的价格是铁的3倍,问底面半径多大时桶的总造价最小?
的有铝合金盖的圆柱形铁桶,已知单位面积铝合金的价格是铁的3倍,问底面半径多大时桶的总造价最小? (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.  与科技成本的投入次数
与科技成本的投入次数 的关系是
的关系是 .若水晶产品的销售价格不变,第
.若水晶产品的销售价格不变,第 万元.
万元.

