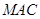题目内容
如图,已知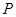 为平行四边形
为平行四边形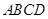 所在平面外一点,
所在平面外一点,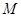 为
为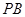 的中点,
的中点,
求证: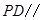 平面
平面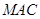 .
.
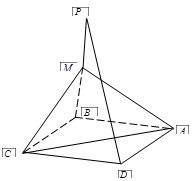
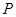 为平行四边形
为平行四边形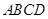 所在平面外一点,
所在平面外一点,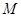 为
为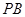 的中点,
的中点,求证:
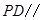 平面
平面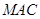 .
.
利用线线平行即可证明线面平行
试题分析:连接
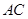 、
、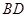 交点为
交点为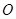 ,连接
,连接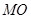 ,则
,则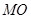 为
为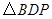 的中位线,
的中位线,
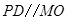 .
.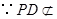 平面
平面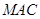 ,
,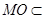 平面
平面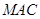 ,
,
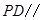 平面
平面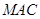
点评:线面平行的判定方法:依据定义和反证法;依判定定理;依面面平行.

练习册系列答案
相关题目
题目内容
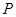 为平行四边形
为平行四边形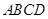 所在平面外一点,
所在平面外一点,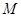 为
为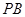 的中点,
的中点,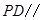 平面
平面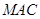 .
.
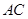 、
、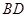 交点为
交点为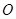 ,连接
,连接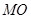 ,则
,则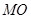 为
为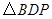 的中位线,
的中位线,
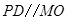 .
.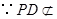 平面
平面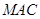 ,
,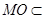 平面
平面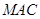 ,
,
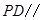 平面
平面