题目内容
(本题满分12分)若定义在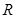 上的函数
上的函数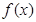 同时满足下列三个条件:
同时满足下列三个条件:
①对任意实数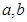 均有
均有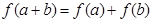 成立;
成立;
②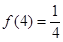 ; ③当
; ③当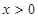 时,都有
时,都有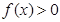 成立。
成立。
(1)求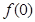 ,
,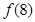 的值;
的值;
(2)求证: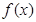 为
为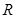 上的增函数
上的增函数
(3)求解关于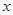 的不等式
的不等式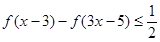 .
.
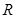 上的函数
上的函数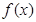 同时满足下列三个条件:
同时满足下列三个条件:①对任意实数
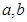 均有
均有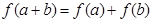 成立;
成立;②
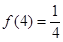 ; ③当
; ③当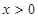 时,都有
时,都有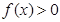 成立。
成立。(1)求
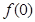 ,
,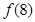 的值;
的值;(2)求证:
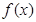 为
为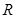 上的增函数
上的增函数(3)求解关于
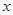 的不等式
的不等式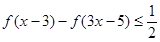 .
.(1)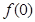 =0,
=0, 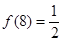 ;(2)证明:见解析;(3)
;(2)证明:见解析;(3)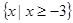 .
.
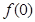 =0,
=0, 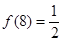 ;(2)证明:见解析;(3)
;(2)证明:见解析;(3)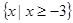 .
.本试题主要是考查了函数的单调性的证明,以及函数与不等式的求解,赋值法求解函数的值。
(1)令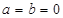 得
得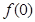 =0,令
=0,令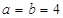 ,得
,得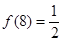
(2)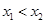 则
则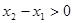 ,则
,则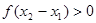 ;利用已知关系式
;利用已知关系式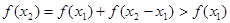 得到证明
得到证明
(3)在第二问的基础上可知得到 ,转换不等式得到
,转换不等式得到
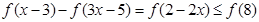 ,进而求解得到结论。
,进而求解得到结论。
解:(1)令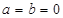 得
得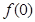 =0,令
=0,令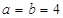 ,得
,得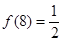
(2)证明:设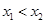 则
则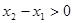 ,则
,则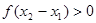 ;
;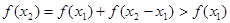 ,故
,故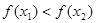 ,
,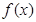 为R上的增函数
为R上的增函数
(3)由已知得 原不等式转化为
原不等式转化为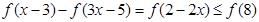 ,结合
,结合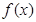 为R上的增函数得:
为R上的增函数得:
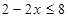 ,解得
,解得 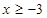 .故原不等式的解集为
.故原不等式的解集为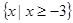 .
.
(1)令
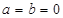 得
得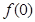 =0,令
=0,令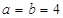 ,得
,得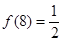
(2)
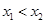 则
则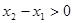 ,则
,则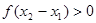 ;利用已知关系式
;利用已知关系式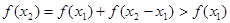 得到证明
得到证明(3)在第二问的基础上可知得到
 ,转换不等式得到
,转换不等式得到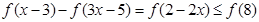 ,进而求解得到结论。
,进而求解得到结论。解:(1)令
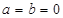 得
得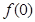 =0,令
=0,令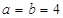 ,得
,得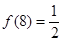
(2)证明:设
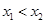 则
则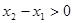 ,则
,则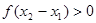 ;
;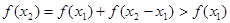 ,故
,故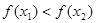 ,
,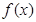 为R上的增函数
为R上的增函数(3)由已知得
 原不等式转化为
原不等式转化为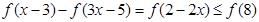 ,结合
,结合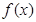 为R上的增函数得:
为R上的增函数得: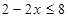 ,解得
,解得 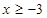 .故原不等式的解集为
.故原不等式的解集为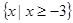 .
.
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
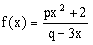 是奇函数,且
是奇函数,且 .
.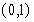 上的单调性,并加以证明.
上的单调性,并加以证明. 
 :
: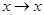 的平方根。
的平方根。
 。
。 :
: 中的数平方。
中的数平方。 的映射的是:
的映射的是: 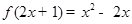 ,则
,则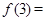 .
. 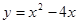 (
( )的值域为( )
)的值域为( )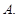



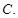



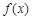 与
与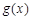 相等的是( )
相等的是( )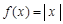 ,
,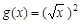
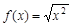 ,
,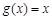
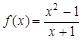 ,
,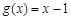
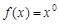 ,
,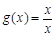
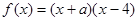 为偶函数,则实数
为偶函数,则实数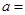
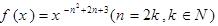 的图像在
的图像在 上单调递增,则
上单调递增,则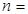 .
.