题目内容
1.已知函数f(x)=x2-(a+1)x+3(x∈R,a∈R).(1)若a=1,写出函数f(x)单调区间;
(2)设函数g(x)=log2x,且x∈[$\frac{1}{2}$,4],若不等式f(g(x))≥$\frac{a+3}{2}$恒成立,求a的取值范围;
(3)已知对任意的x∈(0,+∞)都有lnx≤x-1成立,试利用这个条件证明:当a∈[-2,$\frac{9}{4}$]时,不等式f(x)>ln(x-1)2恒成立.
分析 (1)原函数化简为f(x)=(x-1)2+2,根据二次函数的图象和性质即可得到单调区间;
(2)先求出g(x)的值域,原不等式可化为t2-(a+1)t+3≥$\frac{a+3}{2}$,构造函数h(t),根据二次函数的性质分类讨论,求出函数h(t)的最小值,再解不等式,即可得到答案;
(3)分别根据当x>1或0<x<1,充分利用所给的条件,根据判别式即可证明.
解答 解:(1)当a=1时,f(x)=x2-2x+3=(x-1)2+2,
所以函数的单调减区间为(-∞,1),增区间为[1,+∞).)
(2)因为x∈[$\frac{1}{2}$,4],所以g(x)=log2x∈[-1,2],
设t=g(x) 则∈[-1,2],
∴f(g(x))≥$\frac{a+3}{2}$可化为t2-(a+1)t+3≥$\frac{a+3}{2}$.
令h(t)=t2-(a+1)t+3,其对称轴为t=$\frac{a+1}{2}$,
①当$\frac{a+1}{2}$≤-1,即a≤-3 时,h(t)在[-1,2]上单调递增,
所以h(t)min=h(-1)=1+a+1+3=a+5,
由a+5≥$\frac{a+3}{2}$得a≥-7,
所以-7≤a≤-3;
②当-1<$\frac{a+1}{2}$<2即-3<a<3时,
函数h(t)在(-1,$\frac{a+1}{2}$)上递减,在($\frac{a+1}{2}$,2)上递增,
所以h(t)min=h($\frac{a+1}{2}$)=-$\frac{(a+1)^{2}}{4}$+3.
由-$\frac{(a+1)^{2}}{4}$+3≥$\frac{a+3}{2}$,解得-5≤a≤1.
所以-3<a≤1.
③当$\frac{a+1}{2}$≥2,即a≥3时,函数h(t)在-1,2]递减,
所以h(t)min=h(2)=5-2a,
由5-2a≥$\frac{a+3}{2}$,得a≤$\frac{7}{5}$,舍去.
综上:a∈[-7,1].
(3)?当x>1时,ln(x-1)2=2ln(x-1),
由题意x∈(0,+∞)都有lnx≤x-1成立,
可得x>1时,2ln(x-1)≤2x-4,
∴f(x)-(2x-4)=x2-(a+1)x+3-2x+4=x2-(a+3)x+7,
当a∈[-2,$\frac{9}{4}$]时,△=(a+3)2-28<0恒成立,
所以f(x)-(2x-4)>0恒成立,即f(x)>2x-4恒成立,
所以f(x)>ln(x-1)2恒成立.
?当0<x<1时,ln(x-1)2=2ln(1-x),
由题意可得2ln(1-x)≤-2x,
f(x)-(-2x)=x2-(a-3)x+3,
因为,△=(a-1)2-12,
当当a∈[-2,$\frac{9}{4}$]时,△<0恒成立,
所以f(x)-(-2x)>0,即f(x)>-2x恒成立,
所以f(x)>ln(x-1)2恒成立,
综上,f(x)>ln(x-1)2恒成立.
点评 本题考查了函数的单调性,参数的取值范围,不等式证明,关键是掌握二次函数的性质,需要分类讨论,运算过程大,属于难题.

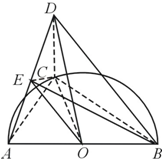 如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.
如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点. 如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=$\sqrt{2}$,给出下列五个结论
如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=$\sqrt{2}$,给出下列五个结论 据统计某校学生在上学路上所需时间最多不超过120分钟,该校随机抽取部分新入校的学生就其上学路上所需时间(单位:分钟)进行调查,并将所得数据绘制成频率分布直方图.
据统计某校学生在上学路上所需时间最多不超过120分钟,该校随机抽取部分新入校的学生就其上学路上所需时间(单位:分钟)进行调查,并将所得数据绘制成频率分布直方图.