题目内容
已知函数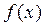 =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x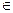 (-∞,-3)
(-∞,-3)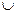 (2,+∞)时,
(2,+∞)时, 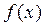 <0,当x
<0,当x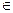 (-3,2)时
(-3,2)时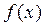 >0 .
>0 .
(1)求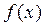 在[0,1]内的值域.
在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.
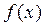 =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x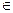 (-∞,-3)
(-∞,-3)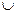 (2,+∞)时,
(2,+∞)时, 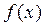 <0,当x
<0,当x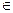 (-3,2)时
(-3,2)时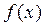 >0 .
>0 .(1)求
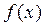 在[0,1]内的值域.
在[0,1]内的值域.(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.
[解] (1)由题意得a<0且ax2+(b-8)x-a-ab=0的根为-3,2
-3+2=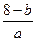 ,(-3)×2=
,(-3)×2=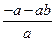
 ,从而a=-3,b=5………4
,从而a=-3,b=5………4
f(x)=-3x2-3x+18,对称轴为x=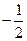 ,可得f(x)∈[12,18]………6
,可得f(x)∈[12,18]………6
(2)由-3x2+5x+c≤0得c≤3x2-5x恒成立,得c≤-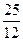 ……10
……10
-3+2=
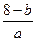 ,(-3)×2=
,(-3)×2=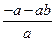
 ,从而a=-3,b=5………4
,从而a=-3,b=5………4f(x)=-3x2-3x+18,对称轴为x=
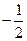 ,可得f(x)∈[12,18]………6
,可得f(x)∈[12,18]………6(2)由-3x2+5x+c≤0得c≤3x2-5x恒成立,得c≤-
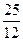 ……10
……10略

练习册系列答案
相关题目
 (
( ),则函数
),则函数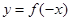 在其定义域上是
在其定义域上是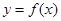 在定义域(-1,1)上是减函数,且
在定义域(-1,1)上是减函数,且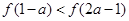 ,则
,则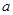 的
的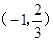
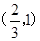
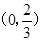
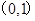
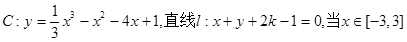 时,
时,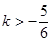 B.
B.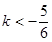 C.
C.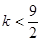 D.
D.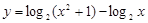 的值域是
的值域是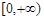
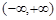
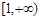
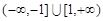
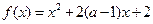 在区间
在区间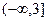 上是减函数,则实数
上是减函数,则实数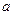 的取值范围为 。
的取值范围为 。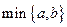 表示
表示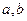 两数中的最小值,若函数
两数中的最小值,若函数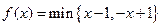 ,则不等式
,则不等式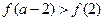 的解集是 .
的解集是 .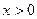 ,则函数
,则函数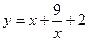 有( )
有( ) 值11
值11