题目内容
【题目】如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y. 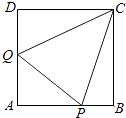
(1)求x,y之间的函数关系式y=f(x);
(2)判断∠PCQ的大小是否为定值?并说明理由;
(3)设△PCQ的面积分别为S,求S的最小值.
【答案】
(1)解:由已知可得PQ=2﹣x﹣y,根据勾股定理有(2﹣x﹣y)2=x2+y2,
化简得:y= ![]() (0<x<1)
(0<x<1)
(2)解:tan∠DCQ=1﹣y,tan∠BCP=1﹣x,
tan(∠DCQ+∠BCP)= ![]() =1
=1
∵∠DCQ+∠BCP∈(0, ![]() ),
),
∴∠DCQ+∠BCP= ![]() ,
,
∴∠PCQ= ![]() ﹣(∠DCQ+∠BCP)=
﹣(∠DCQ+∠BCP)= ![]() ,(定值)
,(定值)
(3)解:S=1﹣ ![]() ﹣
﹣ ![]() (1﹣x)﹣
(1﹣x)﹣ ![]() (1﹣y)=
(1﹣y)= ![]() (x+y﹣xy)=
(x+y﹣xy)= ![]()
![]()
令t=2﹣x,t∈(1,2),
∴S= ![]() (t+
(t+ ![]() )﹣1,
)﹣1,
∴t= ![]() 时,S的最小值为
时,S的最小值为 ![]() ﹣1
﹣1
【解析】(1)由已知可得PQ=2﹣x﹣y,根据勾股定理有(2﹣x﹣y)2=x2+y2 , 即可求x,y之间的函数关系式y=f(x);(2)求得∴∠DCQ+∠BCP= ![]() ,即可判断∠PCQ的大小;(3)表示△PCQ的面积,利用基本不等式求S的最小值.
,即可判断∠PCQ的大小;(3)表示△PCQ的面积,利用基本不等式求S的最小值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目