题目内容
【题目】如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点. 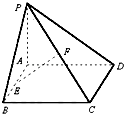
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若∠PDA=45°,求EF与平面ABCD所成的角的大小.
【答案】
(1)解:取PD中点Q,连AQ、QF,则AE∥QF
∴四边形AEFQ为平行四边形
∴EF∥AQ
又∵AQ在平面PAD内,EF不在平面PAD内
∴EF∥面PAD
(2)解:证明∵CD⊥AD,CD⊥PA,PA∩AD=A
PA在平面PAD内,AD在平面PAD内
∴CD⊥面PAD
又∵AQ在平面PAD同
∴CD⊥AQ
∵EF∥AQ
∴CD⊥EF
(3)解:解∵∠PDA=45°
∴△PAD为等腰直角三角形
∴AQ⊥PD
∴∠QAD=45°
即AQ与平面ABCD所成角为45°
又∵AQ∥EF
∴EF与平面ABCD所成角45°.
【解析】(1)取PD中点Q,连AQ、QF,易证EF∥AQ,根据直线与平面平行的判定定理可证得EF∥面PAD;(2)欲证CD⊥EF,可先证直线与平面垂直,CD⊥AD,CD⊥PA,PA∩AD=A,根据直线与平面垂直的判定定理可知CD⊥面PAD,从而得到CD⊥EF;(3)先证∠QAD为AQ与平面ABCD所成角,在三角形QAD中求出此角,再根据AQ∥EF,得到EF与平面ABCD所成的角的大小.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则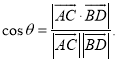 .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目