题目内容
设函数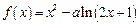 (
(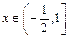 ,
,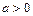 ).
).
(I)若函数 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;
(II)函数 是否有最小值?若有最小值,指出其取得最小值时
是否有最小值?若有最小值,指出其取得最小值时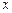 的值,并证明你的结论.
的值,并证明你的结论.
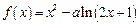 (
(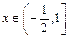 ,
,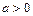 ).
).(I)若函数
 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;(II)函数
 是否有最小值?若有最小值,指出其取得最小值时
是否有最小值?若有最小值,指出其取得最小值时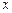 的值,并证明你的结论.
的值,并证明你的结论.解:(1)∵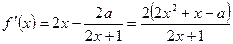 ,
,
∵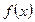 在
在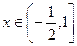 上是减函数,
上是减函数,
∴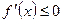 在
在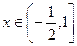 恒成立.
恒成立.
又∵ 当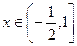 时,
时,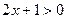 ,
,
 ∴不等式
∴不等式 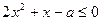 在
在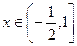 时恒成立,
时恒成立,
即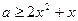 在
在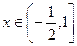 时恒成立,
时恒成立,
设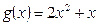 ,
,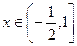 ,则
,则 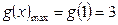 ,∴
,∴ 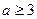
(2)∵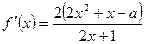 ,令
,令 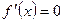 ,
,
解得: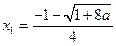 ,
, 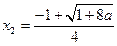 ,
,
由于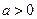 ,∴
,∴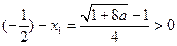 ,
,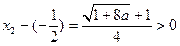 ,
,
∴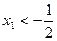 ,
, 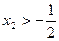 ,
,
① 当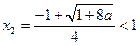 即
即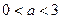 时,在
时,在 上
上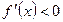 ;在
;在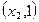 上
上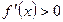 ,
,
∴当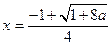 时,函数
时,函数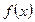 在
在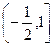 上取最小值.
上取最小值.
② 当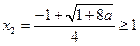 即
即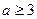 时,在
时,在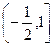 上
上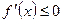 ,
,
∴当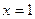 时,函数
时,函数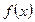 在
在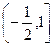 上取最小值.
上取最小值.
由①②可知,当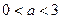 时,函数
时,函数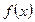 在
在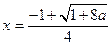 时取最小值;
时取最小值;
当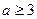 时, 函数
时, 函数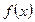 在
在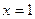 时取最小值
时取最小值
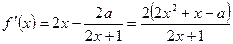 ,
,∵
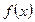 在
在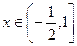 上是减函数,
上是减函数,∴
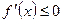 在
在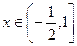 恒成立.
恒成立. 又∵ 当
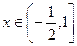 时,
时,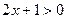 ,
, ∴不等式
∴不等式 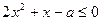 在
在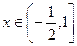 时恒成立,
时恒成立,即
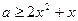 在
在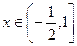 时恒成立,
时恒成立, 设
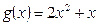 ,
,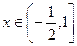 ,则
,则 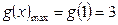 ,∴
,∴ 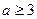
(2)∵
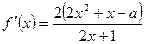 ,令
,令 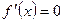 ,
,解得:
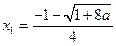 ,
, 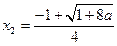 ,
,由于
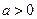 ,∴
,∴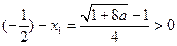 ,
,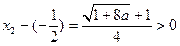 ,
,∴
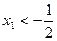 ,
, 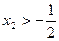 ,
, ① 当
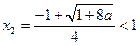 即
即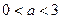 时,在
时,在 上
上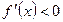 ;在
;在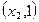 上
上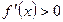 ,
,∴当
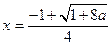 时,函数
时,函数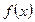 在
在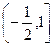 上取最小值.
上取最小值.② 当
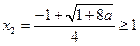 即
即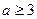 时,在
时,在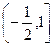 上
上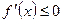 ,
,∴当
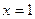 时,函数
时,函数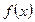 在
在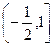 上取最小值.
上取最小值. 由①②可知,当
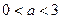 时,函数
时,函数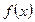 在
在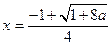 时取最小值;
时取最小值;当
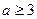 时, 函数
时, 函数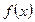 在
在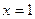 时取最小值
时取最小值略

练习册系列答案
相关题目
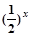
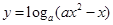 在区间
在区间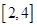 上是增函数,则实数
上是增函数,则实数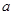 的取值范围是
的取值范围是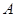 、
、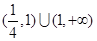
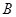 、
、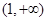
 、
、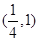
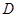 、
、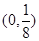
 时,
时, ⊙
⊙ =
= 时,
时, ,则函数
,则函数 =
= 1⊙
1⊙

 ),
), 的最大值等于 ( )
的最大值等于 ( )


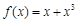 ,
,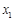 ,
,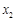 ,
, ,
,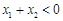 ,
,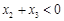 ,
,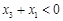 ,则
,则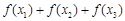 的值( )
的值( )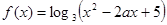 在区间
在区间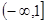 内单调递减,则
内单调递减,则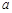 的取值范围是( )
的取值范围是( )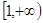
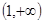
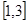
 ,求函数
,求函数 的最小值。
的最小值。 在实数集R上是减函数,则k的范围是__________________;
在实数集R上是减函数,则k的范围是__________________;