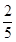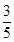题目内容
(本小题满分12分)某同学先后随机抛掷两枚正方体骰子,其中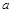 表示第1枚骰子出现的点数,
表示第1枚骰子出现的点数,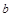 表示第2枚骰子出现的点数.
表示第2枚骰子出现的点数.
(1)求点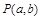 满足
满足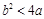 的概率;
的概率;
(2)当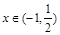 时,求函数
时,求函数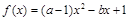 为单调函数的概率.
为单调函数的概率.
 表示第1枚骰子出现的点数,
表示第1枚骰子出现的点数, 表示第2枚骰子出现的点数.
表示第2枚骰子出现的点数.(1)求点
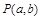 满足
满足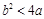 的概率;
的概率;(2)当
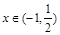 时,求函数
时,求函数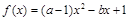 为单调函数的概率.
为单调函数的概率. (1)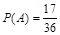 .(2)
.(2) 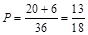 .
.
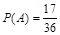 .(2)
.(2) 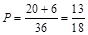 .
.(1)由题意知本题是一个古典概型,试验发生包含的基本事件总数为6×6,满足条件的事件当x=1,2,3,4,5,6挨个列举出基本事件的结果,满足条件的事件有17个基本事件,所以概率为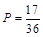 .
.
(2) 本小题也是一个古典概型,试验发生包含的基本事件总数为6×6,满足条件的事件当x=1,2,3,4,5,6挨个列举出基本事件的结果,找满足条件的事件时要分a=1和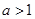 两种情况考虑共有26个基本事件
两种情况考虑共有26个基本事件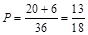
解:(1)每颗骰子出现的点数都有6种情况,所以基本事件的总个数为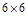 =36.
=36.
记“点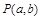 满足
满足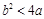 ”为事件
”为事件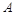 ,则可知事件
,则可知事件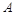 有17个基本事件:
有17个基本事件:
(1,1),(2,1)(2,2),(3,1),(3, 2),(3,3),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4).
故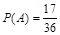 .
.
(2)记数对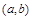 为两次出现的点数情况.当
为两次出现的点数情况.当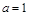 时,函数
时,函数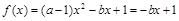 为单调函数,此时符合题意的点为:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),共6个;当
为单调函数,此时符合题意的点为:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),共6个;当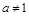 时,即
时,即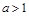 ,函数
,函数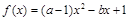 为二次函数,开口向上,其对称轴为
为二次函数,开口向上,其对称轴为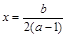 ,要使函数
,要使函数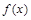 在
在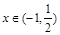 上为单调函数,只需
上为单调函数,只需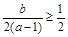 即可,即
即可,即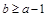 ,
,
则符合题意的点有:
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(3,3),(3,4),(3,5),(3,6),(4,3),(4,4),(4,5),(4,6),(5,4),(5,5),(5,6),(6,5),(6,6)共20个.
故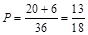 . ………………………………12分
. ………………………………12分
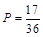 .
.(2) 本小题也是一个古典概型,试验发生包含的基本事件总数为6×6,满足条件的事件当x=1,2,3,4,5,6挨个列举出基本事件的结果,找满足条件的事件时要分a=1和
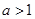 两种情况考虑共有26个基本事件
两种情况考虑共有26个基本事件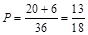
解:(1)每颗骰子出现的点数都有6种情况,所以基本事件的总个数为
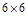 =36.
=36.记“点
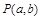 满足
满足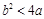 ”为事件
”为事件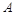 ,则可知事件
,则可知事件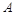 有17个基本事件:
有17个基本事件:(1,1),(2,1)(2,2),(3,1),(3, 2),(3,3),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4).
故
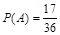 .
.(2)记数对
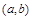 为两次出现的点数情况.当
为两次出现的点数情况.当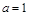 时,函数
时,函数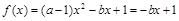 为单调函数,此时符合题意的点为:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),共6个;当
为单调函数,此时符合题意的点为:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),共6个;当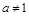 时,即
时,即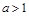 ,函数
,函数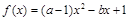 为二次函数,开口向上,其对称轴为
为二次函数,开口向上,其对称轴为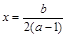 ,要使函数
,要使函数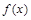 在
在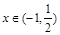 上为单调函数,只需
上为单调函数,只需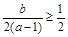 即可,即
即可,即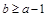 ,
,则符合题意的点有:
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(3,3),(3,4),(3,5),(3,6),(4,3),(4,4),(4,5),(4,6),(5,4),(5,5),(5,6),(6,5),(6,6)共20个.
故
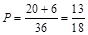 . ………………………………12分
. ………………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率; 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率; 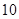 的等边
的等边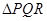 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形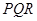 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形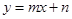 ,设
,设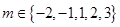 ,
,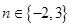 ,则函数
,则函数