题目内容
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 与
与![]() 分别沿
分别沿![]() 向上翻折,使
向上翻折,使![]() 重合,则形成的三棱锥的外接球的表面积为_______.
重合,则形成的三棱锥的外接球的表面积为_______.

【答案】![]()
【解析】
判定三棱锥的形状,确定外接球的球心位置,找出半径并求解,然后求出球的表面积.
![]() 重合为点P,∵∠DAB=60°∴三棱锥P﹣DCE各边长度均为
重合为点P,∵∠DAB=60°∴三棱锥P﹣DCE各边长度均为![]()
∴三棱锥P﹣DCE为正三棱锥 P点在底面DCE的投影为等边△DCE的中心,设中心为O
∴OD=OE=OC=![]()
在直角△POD中:OP2=PD2﹣OD2=![]()
OP=![]()
∵外接球的球心必在OP上,设球心位置为O',
则O'P=O'D 设O'P=O'D=R
则在直角△OO'D中:OO'2+OD2=O'D2,
(OP﹣O'P)2+OD2=O'D2(![]() ﹣R)2+(
﹣R)2+(![]() )2=R2,R=
)2=R2,R=![]() ,
,
∴面积为4![]()
![]() .
.
故答案为:![]() 。
。

【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
| 0.2 | 0.3 | 0.3 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为300元;分4期或5期付款,其利润为400元,![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件![]() :“购买该商品的3位顾客中,至少有1位采用期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用期付款”的概率![]() ;
;
(2)求![]() 的分布列、期望和方差.
的分布列、期望和方差.
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
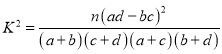 (其中
(其中 ![]() )
)

