题目内容
已知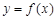 是定义在R上的函数,且对任意
是定义在R上的函数,且对任意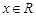 ,都有
,都有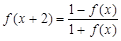 ,又
,又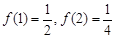 ,则
,则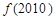 等于( )
等于( )
A.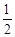 | B.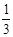 | C.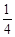 | D.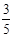 |
C
解析试题分析:根据题意,由于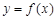 是定义在R上的函数,且对任意
是定义在R上的函数,且对任意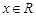 ,都有
,都有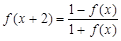 ,同时结合条件
,同时结合条件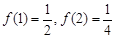 ,那么可知f(4)=
,那么可知f(4)=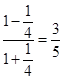 , f(6)=
, f(6)=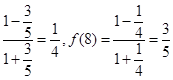 ,即偶数中4的倍数对应的为
,即偶数中4的倍数对应的为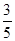 ,不是4的倍数对应的值为
,不是4的倍数对应的值为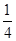 而2010不能被4整除,故f(2010)=
而2010不能被4整除,故f(2010)=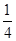 .故选C
.故选C
考点:函数的周期性的运用
点评:解决的关键是根据已知的关系式来推导得到函数的周期性即可,属于基础题。

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
若函数 的零点与
的零点与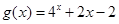 的零点之差的绝对值不超过
的零点之差的绝对值不超过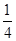 ,则
,则 可以是
可以是
A. =4x-1 =4x-1 | B. =(x-1)2 =(x-1)2 |
C. =ex-2 =ex-2 | D.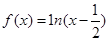 |
下列函数中,在 内为增函数的是( )
内为增函数的是( )
A. | B. |
C. | D. |
已知函数f(x)=ax-x-a(a>0,a≠1),那么函数f(x)的零点个数是
| A.0个 | B.1个 | C.2个 | D.至少1个 |
函数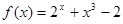 在区间(0,1)内的零点个数是 ( )
在区间(0,1)内的零点个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
函数 是【 】.
是【 】.
A.最小正周期为 的奇函数 的奇函数 | B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 | D.最小正周期为 的偶函数 的偶函数 |
已知函数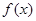 对定义域
对定义域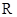 内的任意
内的任意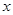 都有
都有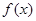 =
=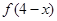 ,且当
,且当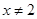 时其导函数
时其导函数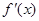 满足
满足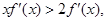 若
若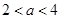 则
则
A.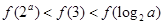 | B.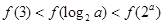 |
C.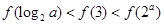 | D.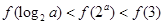 |
设函数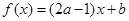 是
是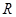 上的减函数,则有( )
上的减函数,则有( )
A.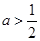 | B.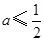 | C.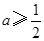 | D.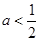 |
 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( )