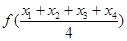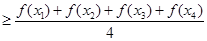题目内容
若函数 的零点与
的零点与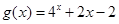 的零点之差的绝对值不超过
的零点之差的绝对值不超过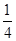 ,则
,则 可以是
可以是
A. =4x-1 =4x-1 | B. =(x-1)2 =(x-1)2 |
C. =ex-2 =ex-2 | D.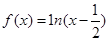 |
A.
解析试题分析: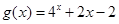 ,根据表达式可知其为增函数。
,根据表达式可知其为增函数。
g(0)=-1,g(0.25)=-0.086,g(0.5)=1,所以零点在(0.25,0.5)之间。
为使零点之差绝对值不超过0.25,函数f(x)的零点应在(0,0.75)之间。
考察知:A. =4x-1的零点0.25,B.
=4x-1的零点0.25,B. =(x-1)2的零点1,C.
=(x-1)2的零点1,C.  =ex-2的零点0,D.
=ex-2的零点0,D. 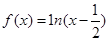 的零点1.5,所以应选A。
的零点1.5,所以应选A。
考点:本题主要考查函数零点的概念,函数零点存在定理。
点评:中档题,本题解题思路比较明确,注意应用函数零点存在定理,判断函数零点所在区间。本题计算量较大。

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
函数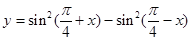 的值域是
的值域是
A.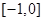 | B.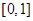 | C.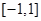 | D.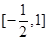 |
当0< ≤
≤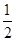 时,
时,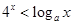 ,则a的取值范围是
,则a的取值范围是
A.(0, ) ) | B.( ,1) ,1) | C.(1,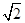 ) ) | D.(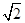 ,2) ,2) |
已知函数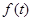 是奇函数且是
是奇函数且是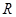 上的增函数,若
上的增函数,若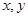 满足不等式
满足不等式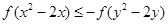 ,则
,则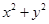 的最大值是( )
的最大值是( )
A. | B.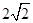 | C.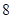 | D.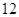 |
已知非零向量 ,
,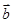 满足
满足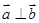 ,则函数
,则函数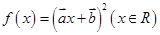 是 ( )
是 ( )
| A.偶函数 | B.奇函数 |
| C.既是奇函数又是偶函数 | D.非奇非偶函数 |
如图为函数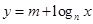 的图象,其中
的图象,其中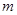 、
、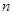 为常数,则下列结论正确( )
为常数,则下列结论正确( )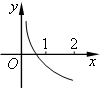
A. , ,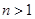 | B. , ,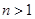 |
C. , , | D. , , |
已知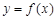 是定义在R上的函数,且对任意
是定义在R上的函数,且对任意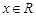 ,都有
,都有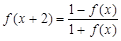 ,又
,又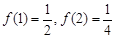 ,则
,则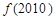 等于( )
等于( )
A.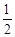 | B.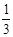 | C.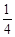 | D.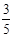 |
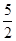 )= ( )
)= ( )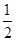 B.-
B.-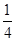 C .
C . 在区间
在区间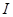 上有定义, 若
上有定义, 若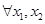
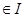 , 都有
, 都有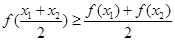 , 则称
, 则称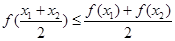 , 则称
, 则称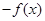 是区间
是区间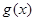 都是区间
都是区间 是区间
是区间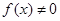 ,则
,则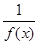 是区间
是区间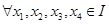 , 则有
, 则有