题目内容
如图,在四棱锥 中,四边形
中,四边形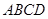 为平行四边形,
为平行四边形, 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若点 为线段
为线段 的中点,求证:.
的中点,求证:.
 中,四边形
中,四边形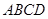 为平行四边形,
为平行四边形, 为
为 上一点,且
上一点,且 .
.(Ⅰ)求证:
 ;
;(Ⅱ)若点
 为线段
为线段 的中点,求证:.
的中点,求证:.

见解析.
(I)证明的关键是 ,
, ,从而证明
,从而证明 ,进而得
,进而得 .
.
(II)证明的关键是证明MN//AF.
证明:(I)由 ,得:
,得:
又 ,故
,故 ,
, ...................6分
...................6分

(Ⅱ)取 中点
中点 连接
连接 则
则

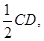 又
又 ,故
,故 ,
,
从而四边形 为平行四边形,进而
为平行四边形,进而 故
故 . ...12分
. ...12分
 ,
, ,从而证明
,从而证明 ,进而得
,进而得 .
.(II)证明的关键是证明MN//AF.
证明:(I)由
 ,得:
,得:
又
 ,故
,故 ,
, ...................6分
...................6分
(Ⅱ)取
 中点
中点 连接
连接 则
则

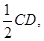 又
又 ,故
,故 ,
,从而四边形
 为平行四边形,进而
为平行四边形,进而 故
故 . ...12分
. ...12分
练习册系列答案
相关题目
 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
, ,
, 是线段
是线段 的中点.
的中点.
 //平面
//平面 ;
; 的大小;
的大小; 上确定一点
上确定一点 ,使得
,使得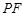 与
与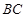 所成的角是
所成的角是 .
.
 是⊙
是⊙ 的直径,
的直径, 垂直于⊙
垂直于⊙ 是圆周上不同于
是圆周上不同于 的任意一点,
的任意一点, .
.
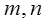 和平面
和平面 则
则 的必要非充分条件是
的必要非充分条件是 且
且
 且
且
 且
且
 与
与 成等角
成等角 ,垂足为O,已知在直角三角形ABC中, BC=1,AC=2,AB=
,垂足为O,已知在直角三角形ABC中, BC=1,AC=2,AB= .该直角三角形在空间做符合以下条件的自由运动:(1)
.该直角三角形在空间做符合以下条件的自由运动:(1) ,(2)
,(2) .则B、O两点间的最大距离为 .
.则B、O两点间的最大距离为 .
 、
、 、
、 、
、 、
、 五个点,且
五个点,且 是正四棱锥,同时球心和
是正四棱锥,同时球心和 的异侧,则
的异侧,则 的取值范围是 .
的取值范围是 . 中,
中, 平面
平面 ,
, ,
, 是
是 的中点.
的中点. 与平面
与平面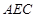 所成的角的正弦值;
所成的角的正弦值; 在线段
在线段 上,二面角
上,二面角 所成角为
所成角为 ,
, ,求
,求 的值.
的值.
 平面ABD,AE=a。
平面ABD,AE=a。 ,求证:AB//平面CDE;
,求证:AB//平面CDE;
