题目内容

17．如图是一个半圆柱与多面体ABB1A1C构成的几何体，平面ABC与半圆柱的下底面共面，且AC⊥BC，P为$\widehat{{A}_{1}{B}_{1}}$上的动点．
（1）证明：PA1⊥平面PBB1；
（2）设半圆柱和多面体ABB1A1C的体积分别为V1，V2，若V1：V2=3π：4，证明：AC=BC．

分析 （1）利用线面垂直的判定定理，即可证明结论；
（2）利用V1：V2=3π：4，确定C到AB的距离=$\frac{1}{2}$AB，即可得出结论．

解答 证明：（1）由题意，A1P⊥B1P，A1P⊥B1B，B1P∩B1B=B1，
∴PA1⊥平面PBB1；
（2）设AB=2a，AA1=h，C到AB的距离为h′，则V1=$\frac{1}{2}π{a}^{2}h$，V2=$\frac{1}{3}×2ah×h′$，
∵V1：V2=3π：4，
∴h′=a，
∵AB=2a，AC⊥BC，
∴AC=BC．

点评 本题考查线面垂直的判定，考查体积的计算，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
7．已知函数f（x）=$\frac{{x}^{2}}{2x-2}$（x≠1），各项同号且均不为零的数列{an}的前n项和Sn满足4Sn•f（$\frac{1}{{a}_{n}}$）=1（n∈N*）．
（1）求f（x）的单调区间；
（2）求数列{an}的通项公式；
（3）求证：（1-$\frac{1}{{a}_{n}}$）an+1＜$\frac{1}{e}$．
8．数列{an}对任意的n∈N*，满足an+1=an +1，a1=12．
（1）求数列{an}的通项公式；
（2）若bn =（$\frac{1}{3}$）${\;}^{{a}_{n}}$+n，求数列{bn}的通项公式及前n项和．
5．已知x，y，z均为正实数，求证：x2+y2+z2≥xy+xz+yz．
12．已知f（x）=ln（x+1）+a（x2-x），a∈R，讨论函数f（x）极值点的个数，并说明理由．
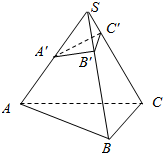2．如图所示，在三棱锥S-ABC中，A′，B′，C′分别在棱SA，SB，SC上，且SA′：SA=1：2，SB′：SB=1：3，SC′：SC=1：4，求VS-ABC与VS-A′B′C′的比．
9．已知a＞0，b＞0，求证：（$\frac{{a}^{2}}{b}$）${\;}^{\frac{1}{2}}$+（$\frac{{b}^{2}}{a}$）${\;}^{\frac{1}{2}}$≥a${\;}^{\frac{1}{2}}$+b${\;}^{\frac{1}{2}}$．
6．把下列程序用程序框图表示出来
7．已知实数x，y满足不等式组$\left\{{\begin{array}{l}{|x|≤π}\\{|y|≤π}\\{sin（x+y）≥0}\end{array}}\right.$，则x+2y的取值范围是[-3π，2π]∪{3π}．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网