题目内容
2.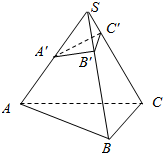 如图所示,在三棱锥S-ABC中,A′,B′,C′分别在棱SA,SB,SC上,且SA′:SA=1:2,SB′:SB=1:3,SC′:SC=1:4,求VS-ABC与VS-A′B′C′的比.
如图所示,在三棱锥S-ABC中,A′,B′,C′分别在棱SA,SB,SC上,且SA′:SA=1:2,SB′:SB=1:3,SC′:SC=1:4,求VS-ABC与VS-A′B′C′的比.
分析 求出C′到平面SA′B′的距离是C到平面SAB的距离的$\frac{1}{4}$,△SA′B′与△SAB的面积的比为1:6,即可求出VS-ABC与VS-A′B′C′的比.
解答 解:由题意,C′到平面SA′B′的距离是C到平面SAB的距离的$\frac{1}{4}$,
∵SA′:SA=1:2,SB′:SB=1:3,
∴△SA′B′与△SAB的面积的比为1:6,
∴VS-ABC与VS-A′B′C′的比为1:24.
点评 本题考查VS-ABC与VS-A′B′C′的比,考查体积的计算,正确运用体积公式是关键.

练习册系列答案
相关题目
14.已知函数f(x)是周期为2的函数,当-1≤x≤1时,f(x)=$\left\{\begin{array}{l}{{x}^{2},-1≤x<0}\\{kx-1,0≤x≤1}\end{array}\right.$,则f($\frac{17}{4}$)=( )
| A. | 0 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
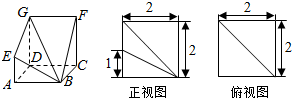 如图,多面体ABCD-EGF中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图,俯视图及相关数据如图.
如图,多面体ABCD-EGF中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图,俯视图及相关数据如图. 如图是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.
如图是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点. 如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证:
如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证: