题目内容
7.已知函数f(x)=$\frac{{x}^{2}}{2x-2}$(x≠1),各项同号且均不为零的数列{an}的前n项和Sn满足4Sn•f($\frac{1}{{a}_{n}}$)=1(n∈N*).(1)求f(x)的单调区间;
(2)求数列{an}的通项公式;
(3)求证:(1-$\frac{1}{{a}_{n}}$)an+1<$\frac{1}{e}$.
分析 (1)求出导数,令导数大于0,可得增区间,令导数小于0,可得减区间;
(2)求得n=1的首项,再将n换为n-1,相减,由通项和前n项和的关系,结合等差数列的通项,即可得到所求通项公式;
(3)运用分析法,可得ln(1+$\frac{1}{n}$)>$\frac{1}{n+1}$,即有ln(1+$\frac{1}{n}$)>$\frac{\frac{1}{n}}{1+\frac{1}{n}}$,构造函数f(x)=ln(1+x)-$\frac{x}{1+x}$(x>0),运用导数判断单调性,即可得证.
解答 解:(1)f(x)=$\frac{{x}^{2}}{2x-2}$(x≠1)的导数为f′(x)=$\frac{{x}^{2}-2x}{2(x-1)^{2}}$,
当x>2或x<0时,f′(x)>0;当0<x<1或1<x<2时,f′(x)<0.
则f(x)的增区间为(-∞,0),(2,+∞),减区间为(0,1),(1,2);
(2)4Sn•f($\frac{1}{{a}_{n}}$)=1,即为2Sn=an-an2,①
当n=1时,2a1=2S1=a1-a12,
解得a1=-1,
将n换为n-1,即有2Sn-1=an-1-an-12,②
①-②,2an=an-an2-(an-1-an-12),
化简可得an+an-1=-(an+an-1)(an-an-1),
即有an-an-1=-1,
则an=-1+(n-1)•(-1)=-n;
(3)要证:(1-$\frac{1}{{a}_{n}}$)an+1<$\frac{1}{e}$,
即证(1+$\frac{1}{n}$)-(n+1)<$\frac{1}{e}$,
即证(1+$\frac{1}{n}$)(n+1)>e,
即证(n+1)ln(1+$\frac{1}{n}$)>1,
即为ln(1+$\frac{1}{n}$)>$\frac{1}{n+1}$,
即有ln(1+$\frac{1}{n}$)>$\frac{\frac{1}{n}}{1+\frac{1}{n}}$,
可令f(x)=ln(1+x)-$\frac{x}{1+x}$(x>0),
f′(x)=$\frac{1}{x+1}$-$\frac{1}{(1+x)^{2}}$=$\frac{x}{(1+x)^{2}}$>0,
f(x)在(0,+∞)递增,即有f(x)>f(0)=0,
即为ln(1+x)>$\frac{x}{1+x}$(x>0),
则ln(1+$\frac{1}{n}$)>$\frac{\frac{1}{n}}{1+\frac{1}{n}}$成立,
故原不等式成立.
点评 本题考查导数的运用:求单调区间,考查数列的通项的求法,注意通项和前n项和的关系,考查不等式的证明,注意运用分析法和构造函数运用单调性证明,属于中档题.

| A. | $(0,\frac{2}{3})$ | B. | $(\frac{2}{3},1)$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{1}{2},\frac{2}{3})$ |
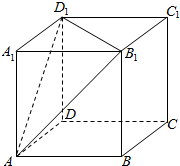 如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$.
如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$. 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示:
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示: 如图是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.
如图是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.