题目内容
3.已知点A,B,C,P在同一平面内,且$\overrightarrow{PQ}$=$\frac{1}{3}$$\overrightarrow{PA}$,$\overrightarrow{QR}$=$\frac{1}{3}$$\overrightarrow{QB}$,$\overrightarrow{RP}$=$\frac{1}{3}$$\overrightarrow{RC}$,则△ABC与△PBC的面积之比是( )| A. | 14:3 | B. | 19:4 | C. | 24:5 | D. | 29:6 |
分析 根据向量共线及面积计算方法,图中所有三角形的面积都可以用△PQR的面积表示出来,计算即可.
解答 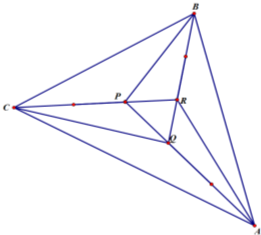 解:如图,∵$\overrightarrow{QR}$=$\frac{1}{3}$$\overrightarrow{QB}$,
解:如图,∵$\overrightarrow{QR}$=$\frac{1}{3}$$\overrightarrow{QB}$,
∴以PQ为底的△PQR与△PQB的高之比为1:3,
所以S△PQB=3S△PQR,即S△PRB=2S△PQR,
∵以BR为底的△PBR与△BCR的高之比为1:3,
∴S△BCR=3S△PBR=6S△PQR,∴S△PBC=2S△PBR=4S△PQR,
同理可得S△ACP=S△ABQ=6S△PQR,
所以$\frac{{S}_{△ABC}}{{S}_{△PBC}}$=$\frac{{S}_{△BCR}+{S}_{△ACP}+{S}_{△ABQ}+{S}_{△PQR}}{{S}_{△PBC}}$
=$\frac{19{S}_{△PQR}}{4{S}_{△PQR}}$
=$\frac{19}{4}$,
故选:B.
点评 本题考查向量共线、面积公式,属于中档题.

练习册系列答案
相关题目
7.已知a,b∈R,且a>b,则下列命题一定成立的是( )
| A. | a>b-1 | B. | a>b+1 | C. | a2>b2 | D. | $\frac{1}{a}<\frac{1}{b}$ |
13.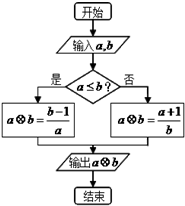 对任意非零实数a,b,定义a⊕b的算法原理如右侧程序框图所示.设a=$\frac{5}{2}$,b=2,则计算机执行该运算后输出的结果是( )
对任意非零实数a,b,定义a⊕b的算法原理如右侧程序框图所示.设a=$\frac{5}{2}$,b=2,则计算机执行该运算后输出的结果是( )
 对任意非零实数a,b,定义a⊕b的算法原理如右侧程序框图所示.设a=$\frac{5}{2}$,b=2,则计算机执行该运算后输出的结果是( )
对任意非零实数a,b,定义a⊕b的算法原理如右侧程序框图所示.设a=$\frac{5}{2}$,b=2,则计算机执行该运算后输出的结果是( )| A. | $\frac{7}{5}$ | B. | $\frac{7}{4}$ | C. | $\frac{7}{3}$ | D. | $\frac{7}{2}$ |